Tetromino

The 5 free tetrominoes

A tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino. The corresponding polycube, called a tetracube, is a geometric shape composed of four cubes connected orthogonally.

A popular use of tetrominoes is in the video game Tetris, where they have been called Tetriminos (spelled with an "i" as opposed to the "o" in "tetromino") since 2001.

The tetrominoes

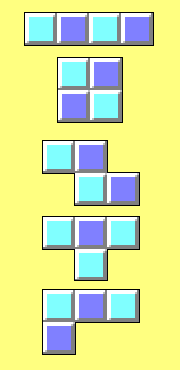The five free tetrominoes, top to bottom I, O, Z, T, L, marked with light and dark squares. As there are a total of 11 light squares and 9 dark squares, it is not possible to pack them into a rectangle (such as ones with 4x5 or 2x10 squares) as any such rectangle has the same number of light and dark squares.

Free tetrominoes

Polyominos are formed by joining unit squares along their edges. A free polyomino is a polyomino considered up to congruence. That is, two free polyominos are the same if there is a combination of translations, rotations, and reflections that turns one into the other.

A free tetromino is a free polyomino made from four squares. There are five free tetrominoes (see figure).

One-sided tetrominoes

One-sided tetrominoes are tetrominoes that may be translated and rotated but not reflected. They are used by, and are overwhelmingly associated with, the game Tetris. There are seven distinct one-sided tetrominoes. Of these seven, three have reflectional symmetry, so it does not matter whether they are considered as free tetrominoes or one-sided tetrominoes. These tetrominoes are:

I (also a "Straight Polyomino"): four blocks in a straight line.
O (also a "Square Polyomino"): four blocks in a 2x2 square.
T (also a "T-Polyomino"): a row of three blocks with one added below the center.

The remaining four tetrominoes exhibit a phenomenon called chirality. These four come in two sets of two. Each of the members of these sets is the reflection of the other. The "L-Polyominos":

J: a row of three blocks with one added below the right side.
L: a row of three blocks with one added below the left side.

The "Skew Polyominos":

S: two stacked horizontal dominoes with the top one offset to the right.
Z: two stacked horizontal dominoes with the top one offset to the left.

As free tetrominoes, J is equivalent to L and S is equivalent to Z. But in two dimensions and without reflections, it is not possible to transform J into L or S into Z.

Fixed tetrominoes

The fixed tetrominoes allow only translation, not rotation or reflection. There are two distinct fixed I-tetrominoes, four J, four L, one O, two S, four T, and two Z, for a total of 19 fixed tetrominoes.

Tiling the rectangle and filling the box with 2D pieces

Although a complete set of free tetrominoes has a total of 20 squares, they cannot be packed into a rectangle, like hexominoes, whereas a full set of pentominoes can be tiled into four different rectangles. The proof resembles that of the mutilated chessboard problem:

A rectangle having 20 squares covered with a checkerboard pattern has 10 each of light and dark squares, but a complete set of free tetrominoes has 11 squares of one shade and 9 of the other (the T tetromino has 3 of one shade and only 1 of the other, while all other tetrominos have 2 of each). Similarly, a complete set of one-sided tetrominoes has 28 squares, requiring a rectangle with 14 squares of each shade, but the set has 15 squares of one shade and 13 of the other.

By extension, any odd number of complete sets of either type cannot fit in a rectangle. However, a bag including two of each free tetromino, which has a total area of 40 squares, can fit in 4x10 and 5x8 square rectangles:

5x8 rectangle

4x10 rectangle

There are many different ways to cover these rectangles. However the 5x8 and the 4x10 rectangles feature distinct properties:

The 5x8 rectangle can be covered in 99392 different ways using 2 complete sets of free tetrominoes (all distinct). Counting only once the solutions connected by symmetries and assuming that the equal tetrominoes are non-distinguishable the number goes down to 783. There are only 13 fundamental solutions which are symmetric under a 180 degrees rotation. There are no solutions with up-down or right-left symmetry.
The 4x10 rectangle can be covered in 57472 different ways. Assuming that the equal tetrominoes are non-distinguishable the number goes down to 449. In this case there are no symmetric solutions.

Likewise, two sets of one-sided tetrominoes can be fit to a rectangle in more than one way. By repeating these rectangles in a row, any even number of complete sets of either type can fit in a rectangle.

The corresponding tetracubes from two complete sets of free tetrominoes can also fit in 2x4x5 and 2x2x10 boxes:

2x4x5 box

 layer 1     :     layer 2

Z Z T t I    :    l T T T i
L Z Z t I    :    l l l t i
L z z t I    :    o o z z i
L L O O I    :    o o O O i

2x2x10 box

      layer 1          :          layer 2

L L L z z Z Z T O O    :    o o z z Z Z T T T l
L I I I I t t t O O    :    o o i i i i t l l l

Etymology

The name "tetromino" is a combination of the prefix tetra- "four" (from Ancient Greek τετρα-), and "domino".

Tetracubes

Each of the five free tetrominoes has a corresponding tetracube, which is the tetromino extruded by one unit. J and L are the same tetracube, as are S and Z, because one may be rotated around an axis parallel to the tetromino's plane to form the other. Three more tetracubes are possible, all created by placing a unit cube on the bent tricube:

Right screw: unit cube placed on top of clockwise side. Chiral in 3D.(Letter D in the diagrams below)
Left screw: unit cube placed on top of anticlockwise side. Chiral in 3D. (Letter S in the diagrams below)
Branch: unit cube placed on bend. Not chiral in 3D. (Letter B in the diagrams below)

Filling the box with 3D pieces

In 3D, these eight tetracubes (suppose each piece consists of four cubes, L and J are the same, Z and S are the same) can fit in a 4x4x2 or 8x2x2 box. The following is one of the solutions. D, S and B represent right screw, left screw and branch point, respectively:

4x4x2 box

layer 1  :  layer 2

S T T T  :  S Z Z B
S S T B  :  Z Z B B
O O L D  :  L L L D
O O D D  :  I I I I

8x2x2 box

    layer 1     :     layer 2

D Z Z L O T T T : D L L L O B S S
D D Z Z O B T S : I I I I O B B S

If chiral pairs (D and S) are considered as identical, the remaining seven pieces can fill a 7x2x2 box. (C represents D or S.)

   layer 1    :    layer 2

L L L Z Z B B : L C O O Z Z B
C I I I I T B : C C O O T T T

Soma cube

COMMENTS