
- Chess World Cup
- FIDE Grand Prix
- Olympiad
- World Championship
- List of strong tournaments
- List of world championships

- Checkmate patterns
- Chess openings
- Chess strategy
- Chess tactics
- Chess theory
- Endgames
- Pawn structure
- Problems/Compositions












A chess puzzle is a puzzle in which knowledge of the pieces and rules of chess is used to solve logically a chess-related problem. The longstanding popularity of chess has paved the way for a rich tradition of such chess-related puzzles and composed problems, which assume a familiarity with the pieces and rules of chess, but can set different objectives than a standard game.
Some chess puzzles may derive from studies which were intended to help a student of the game learn how to seal a victory, but have since evolved into an entirely separate art.
Examples of a chess puzzle include deducing the last move played, the location of a missing piece, or whether a player has lost the right to castle. Sometimes the objective is antithetical to normal chess, such as helping (or even compelling) the opponent to checkmate one's own king.
Read main article: Chess problem
Whereas the term chess puzzle refers broadly to any puzzle involving aspects of chess, a chess problem is an orthodox puzzle (see below) in which one must play and win or draw a game, starting with a certain composition of pieces on the chess board, and playing within the standard rules of chess.
Orthodox chess problems involve positions that can arise from actual game play (although the process of getting to that position may be unrealistic). The most common orthodox chess puzzle takes the form of checkmate in n moves. The puzzle positions are seldom similar to positions from actual play, and the challenge is not to find a winning move, but rather to find the (usually unique) move which forces checkmate as rapidly as possible.
Heterodox chess problems involve conditions that are impossible with normal play, such as multiple kings or chess variants, while fairy chess problems employ pieces not used in orthodox chess, such as the amazon (a piece combining the powers of the queen and the knight).
Chess puzzles can also be regular positions from a game (with normal rules), usually meant as training positions, tactical or positional, from all phases of the game (openings, middlegame of endings). These are known as tactical puzzles. They can range from a simple "Mate in one" combination to a complex attack on the opponent's king. Solving tactical chess puzzles is a very common chess teaching technique. Although it is unlikely that the same position will occur in a game the student plays, the recognition of certain patterns can help to find a good move or plan in another position.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Solitaire Chess is a chess puzzle produced by ThinkFun. The puzzle is played on 4x4 board. The starting position contains several chess pieces. The solver may play capturing moves only. The goal is to achieve a final position that contains only a single piece (similar to peg solitaire). There are no pawn promotions and the king can be captured as other pieces.
An example of Solitaire Chess puzzle is shown at the right. The solution is: 1.Nxb2, 2.Rxb2, 3.Rxb3.
| a | b | c | d | e | f | g | h | ||
| 8 |

  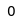 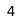    |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Chess miner is a chess puzzle, where the goal is to deduce the location of invisible pieces based on information about how many times certain squares are attacked. For example, in the position at right, the challenge is to place a white king, queen, rook, knight, and bishop in the five marked squares so that the squares with numbers in them are attacked zero and four times respectively. The solution is to place the queen at a1 (the only place where it doesn't attack a6), king at d6 (the only place where it attacks c6), rook at c8, bishop at a4 and knight at a7.
Some chess problems, like the Eight queens puzzle or the Knight's Tour, have connections to mathematics, especially to graph theory and combinatorics. Many famous mathematicians have studied such problems, including Euler, Legendre, and Gauss. Besides finding a solution to a particular puzzle, mathematicians are usually interested in counting the total number of possible solutions, finding solutions with certain properties, and generalization of the problems to nxn or rectangular boards.