- Chess problem
- Chess puzzle
- Eight queens puzzle
- KenKen
- Mahjong solitaire
- Peg solitaire
- Pentomino
- Prisoners and hats puzzle
- Rubik's Cube
- Tangram
- Three cups problem
- Tiling puzzle
- Tsumego
- Tsumeshogi
A dissection puzzle, also called a transformation puzzle or Richter Puzzle, is a tiling puzzle where a set of pieces can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of dissection puzzle. Puzzles may include various restraints, such as hinged pieces, pieces that can fold, or pieces that can twist. Creators of new dissection puzzles emphasize using a minimum number of pieces, or creating novel situations, such as ensuring that every piece connects to another with a hinge.
Ostomachion is a dissection puzzle attributed to ArchimedesDissection puzzles are an early form of geometric puzzle. The earliest known descriptions of dissection puzzles are from the time of Plato (427-347 BCE) in Ancient Greece, and involve the challenge of turning two equal squares into one larger square using four pieces. Other ancient dissection puzzles were used as graphic depictions of the Pythagorean theorem (see square trisection). A famous ancient Greek dissection puzzle is the Ostomachion, a mathematical treatise attributed to Archimedes; now the two equal squares are turned into one square in fourteen pieces by subdivision of the previous four pieces.
In the 10th century, Arabic mathematicians used geometric dissections in their commentaries on Euclid's Elements. In the 18th century, Chinese scholar Tai Chen described an elegant dissection for approximating the value of π.
The puzzles saw a major increase in general popularity in the late 19th century when newspapers and magazines began running dissection puzzles. Puzzle creators Sam Loyd in the United States and Henry Dudeney in the United Kingdom were among the most published. Since then, dissection puzzles have been used for entertainment and maths education, and creation of complex dissection puzzles is considered an exercise of geometric principles by mathematicians and math students.
A Tangram puzzle, with its pieces in the rectangular "storage" configuration.Some types of dissection puzzle are intended to create a large number of different geometric shapes. The tangram is a popular dissection puzzle of this type. The seven pieces can be configured into one of a few home shapes, such as the large square and rectangle that the pieces are often stored in, to any number of smaller squares, triangles, parallelograms, or esoteric shapes and figures. Some geometric forms are easy to create, while others present an extreme challenge. This variability has ensured the puzzle's popularity.
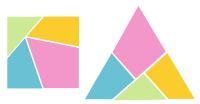The haberdasher's problem, created by Henry Dudeney.Other dissections are intended to move between a pair of geometric shapes, such as a triangle to a square, or a square to a five-pointed star. A dissection puzzle of this description is the haberdasher's problem, proposed in 1907 by Henry Dudeney. The puzzle is a dissection of a triangle to a square, in only four pieces. It is one of the simplest regular polygon to square dissections known, and is now a classic example. It is not known whether a dissection of an equilateral triangle to a square is possible with three pieces.