- Chess problem
- Chess puzzle
- Eight queens puzzle
- KenKen
- Mahjong solitaire
- Peg solitaire
- Pentomino
- Prisoners and hats puzzle
- Rubik's Cube
- Tangram
- Three cups problem
- Tiling puzzle
- Tsumego
- Tsumeshogi
Futoshiki (不等式 futōshiki), or More or Less, is a logic puzzle game from Japan. Its name means "inequality". It is also spelled hutosiki (using Kunrei-shiki romanization).
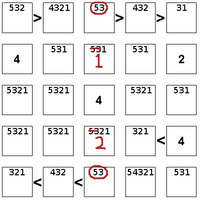The first step to solve the puzzle is to enumerate possible values based on inequalities and non-duplication within rows and columns. Then AB elimination may be usable to narrow down the range of possibilities. As shown here, the top and bottom positions in the center column must contain 5 and 3, so these can be excluded from the second and fourth positions.
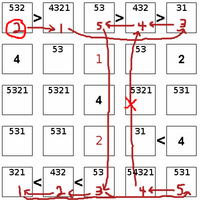Logical deduction within the inequalities can restrict the range of possibilities. As shown here, a 2 in the upper left corner requires a 1 in the second position due to the first inequality; but a 1 in the second position allows only a 3 in the fifth position ... and so on, until we conclude two 4s would need to be placed in the same column. Likewise a 3 in the upper left corner would require the top row to be 3 2 5 4 1 and the bottom again to be 1 2 3 4 5 - leading to the same contradiction. Only a 5 is permissible in the top left corner, from which we deduce 5 4 3 2 1 at top and 1 2 5 4 3 at bottom. The remainder of the solution is simple elimination.The puzzle is played on a square grid, such as 5 x 5. The objective is to place the numbers 1 to 5 (or whatever the dimensions are) such that each row, and column contains each of the digits 1 to 5. Some digits may be given at the start. In addition, inequality constraints are also initially specified between some of the squares, such that one must be higher or lower than its neighbour. These constraints must be honoured as the grid is filled out.
Solving the puzzle requires a combination of logical techniques. Numbers in each row and column restrict the number of possible values for each position, as do the inequalities.
Once the table of possibilities has been determined, a crucial tactic to solve the puzzle involves "AB elimination", in which subsets are identified within a row whose range of values can be determined. For example, if the first two squares within a row must contain 1 or 2, then these numbers can be excluded from the remaining squares. Similarly, if the first three squares must contain 1 or 2; 1 or 3; and 1 or 2 or 3, then those remaining must contain other values (4 and 5 in a 5x5 puzzle).
Another important technique is to work through the range of possibilities in open inequalities. A value on one side of an inequality determines others, which then can be worked through the puzzle until a contradiction is reached and the first value is excluded.
Additionally, many Futoshiki puzzles are promised to possess unique solutions. If this is strictly true, then regions of the form
A . B . . . B . A
cannot be present, unless an inequality or pre-filled number can specify which of the two numbers is B and which number is A, since rotating the four values would produce an alternate, valid solution.
A solved Futoshiki puzzle is a Latin square.
As in the Sudoku case, Futoshiki puzzles harder than those amenable to the above techniques require the use of various types of chain patterns.
The puzzle is published every Saturday in The Guardian and in The Daily Telegraph. It appears daily in The Times " I (newspaper) "(not Saturdays) and the Dundee Courier.