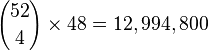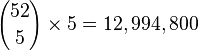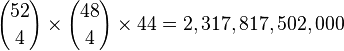Cribbage statistics
Read main article: Cribbage
Some cribbage statistics are
Distinct hands
- There are 12,994,800 possible hands in Cribbage: 52 choose 4 for the hand, and any one of the 48 left as the starter card.
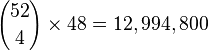
- Another, and perhaps more intuitive way of looking at it, is to say that there are 52 choose 5 different 5-card hands, and any one of those 5 could be the turn-up, or starter card.
Therefore the calculation becomes:
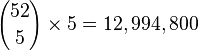
- 1,009,008 (approximately 7.8%) of these score zero points, or 1,022,208 if the hand is the crib.
- Not accounting for suit, there are 14715 unique hands.
Maximum scores
- The highest score for one hand is 29: 555J in hand with the starter 5 of the same suit as the Jack (8 points for four J-5 combinations, 8 points for four 5-5-5 combinations, 12 points for pairs of 5s and one for his nob).
- The second highest score is 28 (hand and starter together comprise any ten-point card plus all four 5s, apart from the 29-point hand above).
- The third highest score is 24 (A7777, 33339, 36666, 44447, 44556, 44566, 45566, 67788 or 77889).
- The highest score as a dealer from the hand and crib is 53. The starter must be a 5, the hand must be J555, with the Jack suit matching the starter (score 29), and the crib must be 4466 (score 24), or vice versa.
- The highest number of points possible (excluding pegging points) in one round is 77. The dealer must score 53, the opponent must then have the other 4466 making another 24 point hand for a total of 77.
- The highest number of points from a hand that has a potential to be a "19 hand" is 15. It is a crib hand of one suit, 46J and another ten card, with a 5 of that suit cut up. The points are 15 for 6, a run for 9, nobs for 10, and a flush for 15. Any of the following cards in an unlike suit yields a "19 hand"; 2,3,7,8,and an unpaired ten card.
- The most points that can be pegged by playing one card is 15, by completing a double pair royal on the last card and making the count 15: 12 for double pair royal, 2 for the 15, and 1 for the last card. This can happen in two ways in a two-player game. The non-dealer must have two ten-value cards and two 2s, and the dealer must have one ten-value card and 722, in which case the play must go: 10-10-10-go; 7-2-2-2-2. For example:
| Player |
Card |
Cumulative |
Score |
Announced |
| Bob |
 |
10 |
|
"ten" |
| Alice |
 |
20 |
|
"twenty" |
| Bob |
 |
30 |
3 points (run) |
"thirty" |
| Alice |
|
|
1 point to Bob (30 for one) |
"go" |
| Alice |
 |
7 |
|
"seven" |
| Bob |
 |
9 |
|
"nine" |
| Alice |
 |
11 |
2 points |
"eleven for two" |
| Bob |
 |
13 |
6 points |
"thirteen for six" |
| Alice |
 |
15 |
15 points (double pair royal,
fifteen, last card) |
"fifteen for fifteen" |
- Alternatively, the players can each have two deuces, with one also holding A-4 and the other two aces. Then play might go 4-A-A-A-2-2-2-2.
- The maximum number of points that can be scored in a single deal by the dealer in a two player game is 78 (pegging + hand + crib):
Non-dealer is dealt 3 3 4 4 5 J and Dealer is dealt 3 3 4 4 5 5. Non-dealer discards J 5 to the crib (as ill-advised as this may be). Dealer discards 5 5 to the crib. Note that the J is suited to the remaining 5. The remaining 5 is cut.
Play is 3 3 3 3 4 4 4 4 go. The dealer scores 29 total peg points.
The dealer's hand is 3 3 4 4 5 = 20
The dealer's crib is J(nobs) 5 5 5 5 = 29
The total score for the dealer is 29 + 20 + 29 = 78.
Note that the correct play for both players is to keep 3 3 4 5 worth 10 points and discarding J 4 & 4 5 to the crib respectively, meaning in reality, this hand would never take place. A more realistic hand would be both players being dealt 3 3 4 4 J J with both discarding J J and a 5 cut. In this case, with pegging as described above, the total score would be 20 (hand) + 21 (crib) + 29 (pegging) = 70 points.
- The maximum number of points that can be scored in a single deal by the non-dealer in a two player game is 48 (pegging + hand), with the following example :
Non-dealer is dealt 5 5 4 4 crib crib and Dealer is dealt 4 4 5 9 crib crib. Cut card is a 6.
Play is 5 5 5 4 4 4 4, with the Non-dealer pegging 24. The Non-dealer scores 24 in the hand for a total of 48 points.
Minimum scores
- The dealer in two-player, 6-card cribbage will always peg at least one point during the play (the pegging round), unless the opponent wins the game before the pegging is finished. If non-dealer is able to play at each turn then dealer must score at least one for "last"; if not, then dealer scores at least one for "go".
- While 19 is generally recognized as "the impossible hand", meaning that there is no combination of 5 cards that will produce a score of 19 points, scores of 25, 26, 27, and greater than 29 are also impossible in-hand point totals. Sometimes if a player scores 0 points in their hand they will claim they have a "19-point hand."
Minimum while holding a five
If a player holds a 5 in their hand, that player is guaranteed at least two points, as shown below:
A 0-point hand must have five distinct cards without forming a run or a fifteen combination. If such a hand includes a 5, it cannot hold any face cards. It also cannot include both an A and a 9; both a 2 and an 8; both a 3 and a 7; or both a 4 and a 6. Since four more cards are needed, exactly one must be taken from each of those sets. Let us run through the possible choices:
- If the hand includes a 9, it cannot hold a 6, so it must hold a 4. Having both a 4 and a 9, it cannot hold a 2, so it must hold an 8. Holding both a 4 and an 8, it cannot hold a 3, so it must hold a 7. But now the hand includes a 7-8 fifteen, which is a contradiction.
- Therefore the hand must include an A. If the hand includes a 7, it now cannot contain an 8, as that would form a 7-8 fifteen. However it cannot hold a 2, as that would form a 7-5-2-A fifteen. This is a contradiction.
- Therefore the hand must include a 3. Either a 2 or a 4 would complete a run, so the hand must therefore include a 6 and an 8. But this now forms an 8-6-A fifteen, which is a contradiction.
Therefore every set of 5 cards including a 5 has a pair, a run, or a fifteen, and thus at least two points.
It is also true that holding both a 2 and a 3, or an A and a 4 (pairs of cards adding up to five) also guarantees a non-zero score:
- If a hand includes both a 2 and a 3 and is to score 0 points, it cannot have a face card, an A, a 4, or a 5. This requires three cards from the 6, 7, 8, and 9, and any such selection will include a fifteen.
- If a hand includes both an A and a 4 and is to score 0 points, it cannot have a face card or a 5. It also cannot have both a 2 and a 3; both a 6 and a 9; or both a 7 and an 8. If the hand includes a 2, it cannot have a 9 (9-4-2 fifteen). Thus it must have a 6. It then cannot have an 8 (8-4-2-A fifteen) or a 7 (7-6-2 fifteen). If, however, the hand includes a 3, it cannot include an 8 (8-4-3 fifteen) or a 7 (7-4-3-A fifteen). These are all contradictions, so every hand containing both an A and a 4 scores at least two points.
Odds
- The odds of getting a 28 hand in a two-player game are 1 in 15,028.
- The odds of getting a perfect 29 hand in a two-player game are 1 in 216,580.
- The odds of getting a perfect 29 hand in a three- or four-player game are 1 in 649,740.
Scoring Breakdown
| Score |
Number of hands
(out of 12,994,800) |
Percentage of hands |
Percentage of hands at least as high |
| 0 |
1009008 |
7.7647 |
100 |
| 1 |
99792 |
0.7679 |
92.2353 |
| 2 |
2813796 |
21.6532 |
91.4674 |
| 3 |
505008 |
3.8862 |
69.8142 |
| 4 |
2855676 |
21.9755 |
65.928 |
| 5 |
697508 |
5.3676 |
43.9525 |
| 6 |
1800268 |
13.8538 |
38.5849 |
| 7 |
751324 |
5.7817 |
24.7311 |
| 8 |
1137236 |
8.7515 |
18.9494 |
| 9 |
361224 |
2.7798 |
10.1979 |
| 10 |
388740 |
2.9915 |
7.4181 |
| 11 |
51680 |
0.3977 |
4.4266 |
| 12 |
317340 |
2.4421 |
4.0289 |
| 13 |
19656 |
0.1513 |
1.5868 |
| 14 |
90100 |
0.6934 |
1.4355 |
| 15 |
9168 |
0.0706 |
0.7421 |
| 16 |
58248 |
0.4482 |
0.6715 |
| 17 |
11196 |
0.0862 |
0.2233 |
| 18 |
2708 |
0.0208 |
0.1371 |
| 19 |
0 |
0 |
0.1163 |
| 20 |
8068 |
0.0621 |
0.1163 |
| 21 |
2496 |
0.0192 |
0.0542 |
| 22 |
444 |
0.0034 |
0.0350 |
| 23 |
356 |
0.0027 |
0.0316 |
| 24 |
3680 |
0.0283 |
0.0289 |
| 25 |
0 |
0 |
0.0006 |
| 26 |
0 |
0 |
0.0006 |
| 27 |
0 |
0 |
0.0006 |
| 28 |
76 |
0.0006 |
0.0006 |
| 29 |
4 |
0.00003 |
0.00003 |
- Mean = 4.7692
- Standard deviation = 3.1254
- Skewness = 0.9039
- Excess kurtosis = 1.4599
Note that these statistics do not reflect frequency of occurrence in 5 or 6-card play. For 6-card play the mean for non-dealer is 7.8580 with standard deviation 3.7996, and for dealer is 7.7981 and 3.9082 respectively. The means are higher because the player can choose those four cards that maximize their point holdings. For 5-card play the mean is about 5.4.
Slightly different scoring rules apply in the crib - only 5-point flushes are counted, in other words you need to flush all cards including the turn-up and not just the cards in the crib. Because of this, a slightly different distribution is observed:
Scoring Breakdown (crib/box hands only)
| Score |
Number of hands (+/- change from non-crib distribution)
(out of 12,994,800) |
Percentage of hands |
Percentage of hands at least as high |
| 0 |
1022208 (+13200) |
7.8663 |
100 |
| 1 |
99792 (0) |
0.7679 |
92.1337 |
| 2 |
2839800 (+26004) |
21.8534 |
91.3658 |
| 3 |
508908 (+3900) |
3.9162 |
69.5124 |
| 4 |
2868960 (+13284) |
22.0778 |
65.5962 |
| 5 |
703496 (+5988) |
5.4137 |
43.5184 |
| 6 |
1787176 (-13092) |
13.7530 |
38.1047 |
| 7 |
755320 (+3996) |
5.8125 |
24.3517 |
| 8 |
1118336 (-18900) |
8.6060 |
18.5393 |
| 9 |
358368 (-2856) |
2.7578 |
9.9332 |
| 10 |
378240 (-10500) |
2.9107 |
7.1755 |
| 11 |
43880 (-7800) |
0.3377 |
4.2648 |
| 12 |
310956 (-6384) |
2.3929 |
3.9271 |
| 13 |
16548 (-3108) |
0.1273 |
1.5342 |
| 14 |
88132 (-1968) |
0.6782 |
1.4068 |
| 15 |
9072 (-96) |
0.0698 |
0.7286 |
| 16 |
57288 (-960) |
0.4409 |
0.6588 |
| 17 |
11196 (0) |
0.0862 |
0.2179 |
| 18 |
2264 (-444) |
0.0174 |
0.1318 |
| 19 |
0 (0) |
0 |
0.1144 |
| 20 |
7828 (-240) |
0.0602 |
0.1144 |
| 21 |
2472 (-24) |
0.0190 |
0.0541 |
| 22 |
444 (0) |
0.0034 |
0.0351 |
| 23 |
356 (0) |
0.0027 |
0.0317 |
| 24 |
3680 (0) |
0.0283 |
0.0289 |
| 25 |
0 (0) |
0 |
0.0006 |
| 26 |
0 (0) |
0 |
0.0006 |
| 27 |
0 (0) |
0 |
0.0006 |
| 28 |
76 (0) |
0.0006 |
0.0006 |
| 29 |
4 (0) |
0.00003 |
0.00003 |
As above, these statistics do not reflect the true distributions in 5 or 6 card play, since both the dealer and non-dealer will discard tactically in order to maximise or minimise the possible score in the crib/box.
Card combinations
- A hand of four aces (AAAA) is the only combination of cards wherein no flip card will add points to its score.
- There are 71 distinct combinations of card values that add to 15:
Two
cards |
Three
cards |
Four cards |
Five cards |
X5
96
87 |
X4A
X32
95A
942
933 |
86A
852
843
77A
762 |
753
744
663
654
555 |
X3AA
X22A
94AA
932A
9222
85AA |
842A
833A
8322
76AA
752A
743A |
7422
7332
662A
653A
6522
644A |
6432
6333
554A
5532
5442
5433
4443 |
X2AAA
93AAA
922AA
84AAA
832AA
8222A
75AAA |
742AA
733AA
7322A
72222
66AAA
652AA
643AA |
6422A
6332A
63222
553AA
5522A
544AA
5432A |
54222
5333A
53322
4442A
4433A
44322
43332 |
| Note: "X" indicates a card scoring ten: 10, J, Q or K |
Hand and Crib statistics
If both the hand and the crib are considered as a sum (and both are drawn at random, rather than formed with strategy as is realistic in an actual game setting) there are 2,317,817,502,000 (2.3 trillion) 9-card combinations. 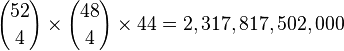
- As stated above, the highest score a dealer can get with both hand and crib considered is 53.
- The only point total between 0 and 53 that is not possible is 51.
Scoring Breakdown
| Score |
Number of hand-crib pairs
(out of 2,317,817,502,000) |
Percentage of hand-crib pairs |
Percentage of hand-crib pairs at least as high |
| 0 |
14485964652 |
0.624983 |
100 |
| 1 |
3051673908 |
0.131662 |
99.375017 |
| 2 |
80817415668 |
3.486789 |
99.243356 |
| 3 |
23841719688 |
1.028628 |
95.756566 |
| 4 |
190673505252 |
8.226424 |
94.727938 |
| 5 |
70259798952 |
3.031291 |
86.501514 |
| 6 |
272593879188 |
11.7608 |
83.470222 |
| 7 |
121216281624 |
5.22976 |
71.709422 |
| 8 |
290363331432 |
12.527446 |
66.479663 |
| 9 |
151373250780 |
6.530853 |
53.952217 |
| 10 |
254052348948 |
10.960843 |
47.421364 |
| 11 |
141184445960 |
6.091267 |
36.460521 |
| 12 |
189253151324 |
8.165145 |
30.369254 |
| 13 |
98997926340 |
4.27117 |
22.204109 |
| 14 |
127164095564 |
5.486372 |
17.932939 |
| 15 |
59538803512 |
2.568744 |
12.446567 |
| 16 |
77975659056 |
3.364185 |
9.877823 |
| 17 |
32518272336 |
1.402969 |
6.513638 |
| 18 |
42557293000 |
1.836093 |
5.110669 |
| 19 |
17654681828 |
0.761694 |
3.274576 |
| 20 |
22185433540 |
0.957169 |
2.512881 |
| 21 |
8921801484 |
0.384923 |
1.555712 |
| 22 |
10221882860 |
0.441013 |
1.17079 |
| 23 |
4016457976 |
0.173286 |
0.729776 |
| 24 |
5274255192 |
0.227553 |
0.55649 |
| 25 |
1810154696 |
0.078097 |
0.328938 |
| 26 |
2305738180 |
0.099479 |
0.25084 |
| 27 |
750132024 |
0.032364 |
0.151361 |
| 28 |
1215878408 |
0.052458 |
0.118998 |
| 29 |
401018276 |
0.017302 |
0.06654 |
| 30 |
475531940 |
0.020516 |
0.049238 |
| 31 |
184802724 |
0.007973 |
0.028722 |
| 32 |
233229784 |
0.010062 |
0.020749 |
| 33 |
82033028 |
0.003539 |
0.010686 |
| 34 |
71371352 |
0.003079 |
0.007147 |
| 35 |
19022588 |
0.000821 |
0.004068 |
| 36 |
44459120 |
0.001918 |
0.003247 |
| 37 |
9562040 |
0.000413 |
0.001329 |
| 38 |
10129244 |
0.000437 |
0.000916 |
| 39 |
1633612 |
0.00007 |
0.000479 |
| 40 |
5976164 |
0.000258 |
0.000409 |
| 41 |
1517428 |
0.000065 |
0.000151 |
| 42 |
600992 |
0.000026 |
0.000085 |
| 43 |
127616 |
0.000006 |
0.00006 |
| 44 |
832724 |
0.000036 |
0.000054 |
| 45 |
222220 |
0.00001 |
0.000018 |
| 46 |
42560 |
0.000002 |
0.000009 |
| 47 |
24352 |
0.000001 |
0.000007 |
| 48 |
119704 |
0.000005 |
0.000006 |
| 49 |
6168 |
0 |
0 |
| 50 |
384 |
0 |
0 |
| 51 |
0 |
0 |
0 |
| 52 |
4320 |
0 |
0 |
| 53 |
288 |
0 |
0 |
- Mean: 9.50397
- Median: 9
- Mode: 8
Read more:
- Cribbage (rules)
- Cribbage (strategy)
COMMENTS