Heptomino

The 108 free heptominoes

A heptomino (or 7-omino) is a polyomino of order 7, that is, a polygon in the plane made of 7 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hept(a)-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free heptominoes. When reflections are considered distinct, there are 196 one-sided heptominoes. When rotations are also considered distinct, there are 760 fixed heptominoes.

Symmetry

The figure shows all possible free heptominoes, coloured according to their symmetry groups:

• 84 heptominoes (coloured grey) have no symmetry. Their symmetry group consists only of the identity mapping.
• 9 heptominoes (coloured red) have an axis of reflection symmetry aligned with the gridlines. Their symmetry group has two elements, the identity and the reflection in a line parallel to the sides of the squares.

• 7 heptominoes (coloured green) have an axis of reflection symmetry at 45° to the gridlines. Their symmetry group has two elements, the identity and a diagonal reflection.

• 4 heptominoes (coloured blue) have point symmetry, also known as rotational symmetry of order 2. Their symmetry group has two elements, the identity and the 180° rotation.

• 3 heptominoes (coloured purple) have two axes of reflection symmetry, both aligned with the gridlines. Their symmetry group has four elements, the identity, two reflections and the 180° rotation. It is the dihedral group of order 2, also known as the Klein four-group.
• 1 heptomino (coloured orange) has two axes of reflection symmetry, both aligned with the diagonals. Its symmetry group also has four elements. Its symmetry group is also the dihedral group of order 2 with four elements.

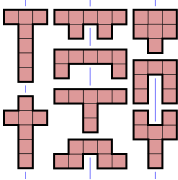
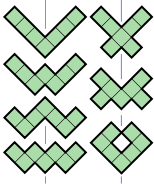
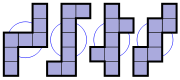
If reflections of a heptomino are considered distinct, as they are with one-sided heptominoes, then the first and fourth categories above would each double in size, resulting in an extra 88 heptominoes for a total of 196. If rotations are also considered distinct, then the heptominoes from the first category count eightfold, the ones from the next three categories count fourfold, and the ones from the last two categories count twice. This results in 84 x 8 + (9+7+4) x 4 + (3+1) x 2 = 760 fixed heptominoes.

Packing and tiling

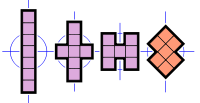
Of the 108 free heptominoes, 101 of them satisfy the Conway criterion and 3 more of them can form a patch satisfying the criterion. Thus, only 4 heptominoes fail to satisfy the criterion and, in fact, these 4 are unable to tessellate the plane.

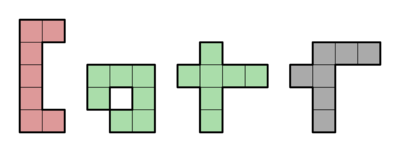Heptominoes incapable of tiling a plane, including the one heptomino with a hole.

Although a complete set of the 108 free heptominoes has a total of 756 squares, it is not possible to tile a rectangle with them. The proof of this is trivial, since there is one heptomino which has a hole. It is also impossible to pack them into a 757-square rectangle with a one-square hole because 757 is a prime number.