
- Tabletop games
- Board games
- Tile-based games
- Turn-based games.html
- Abstract strategy games
- card games
- Connection games
- Mancala games
- Paper-and-pencil games
- Word games



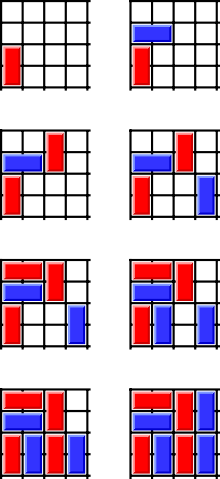 Example of a Cram game. In the normal version, the blue player wins.
Example of a Cram game. In the normal version, the blue player wins.Cram is a mathematical game played on a sheet of graph paper. It is the impartial version of Domineering and the only difference in the rules is that each player may place their dominoes in either orientation, but it results in a very different game. It has been called by many names, including "plugg" by Geoffrey Mott-Smith, and "dots-and-pairs." Cram was popularized by Martin Gardner in Scientific American.
The game is played on a sheet of graph paper, with any set of designs traced out. It is most commonly played on rectangular board like a 6x6 square or a checkerboard, but it can also be played on an entirely irregular polygon or a cylindrical board.
Two players have a collection of dominoes which they place on the grid in turn. A player can place a domino either horizontally or vertically. Contrary to the related game of Domineering, the possible moves are the same for the two players, and Cram is then an impartial game.
As for all impartial games, there are two possible conventions for victory : in the normal game, the first player who cannot move loses, and on the contrary, in the misère version, the first player who cannot move wins.
The winning strategy for normal Cram is simple for even-by-even boards and even-by-odd boards. In the even-by-even case, the second player wins by symmetry play. This means that whichever move Player 1 makes, Player 2 has a corresponding symmetric move across the horizontal and vertical axes. In a sense, player 2 "mimics" the moves made by Player 1. If Player 2 follows this strategy, Player 2 will always make the last move, and thus win the game.
In the even-by-odd case, the first player wins by similar symmetry play. Player 1 places his first domino in the center two squares on the grid. Player 2 then makes his move, but Player 1 can play symmetrically thereafter, thus ensuring a win for Player 1.
It should be noted that symmetry play is a useless strategy in the misère version, because in that case it would only ensure the player that he loses.
Since Cram is an impartial game, the Sprague-Grundy theorem indicates that in the normal version any Cram position is equivalent to a nim-heap of a given size, also called the Grundy value. Some values can be found in Winning Ways for your Mathematical Plays, in particular the 2 x n board, whose value is 0 if n is even and 1 if n is odd.
The symmetry strategy implies that even-by-even boards have a Grundy value of 0, but in the case of even-by-odd boards it only implies a Grundy value greater or equal to 1.
| n x m | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| 4 | 0 | 2 | 0 | 3 | 0 | 1 |
| 5 | - | 0 | 2 | 1 | 1 | ≥1 |
| 6 | - | - | 0 | >3 | 0 | ≥1 |
| 7 | - | - | - | ≥1 | ≥1 | ? |
In 2009, Martin Schneider computed the grundy values up to the 3 x 9, 4 x 5 and 5 x 7 boards. In 2010, Julien Lemoine and Simon Viennot applied to the game of Cram algorithms that were initially developed for the game of Sprouts. It allowed them to compute the grundy-values up to the 3 x 18, 4 x 9 and 5 x 8 boards. They were also able to compute the outcome (but not the grundy-value) of the 5 x 9 and 7 x 7 boards.
The sequence of currently known Grundy values for 3 x n boards, from n=1 to n=18 is: 1, 1, 0, 1, 1, 4, 1, 3, 1, 2, 0, 1, 2, 3, 1, 4, 0, 1. It doesn't show any apparent pattern.
The table below details the known results for boards with both dimensions greater than 3. Since the value of an n x m board is the same as the value of a m x n board, we give only the upper part of the table.
The misère Grundy-value of a game G is defined by Conway in On Numbers and Games as the unique number n such that G+n is a second player win in misère play. Even if it looks very similar to the usual Grundy-value in normal play, it is not as powerful. In particular, it is not possible to deduce the misère Grundy-value of a sum of games only from their respective misère grundy-values.
| n x m | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| 4 | 0 | 0 | 0 | 1 | 1 | 1 |
| 5 | - | 2 | 1 | 1 | ? | ? |
| 6 | - | - | 1 | ? | ? | ? |
In 2009, Martin Schneider computed the misère grundy values up to the 3 x 9, 4 x 6, and 5 x 5 board. In 2010, Julien Lemoine and Simon Viennot extended these results up to the 3 x 15, 4 x 9 and 5 x 7 boards, along with the value of the 6 x 6 board.
The sequence of currently known misère Grundy values for 3 x n boards, from n=1 to n=15 is: 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1. This sequence is conjectured to be periodic of period 3.
The table on the right details the known misère results for boards with both dimensions greater than 3.