
- Tabletop games
- Board games
- Tile-based games
- Turn-based games.html
- Abstract strategy games
- card games
- Connection games
- Mancala games
- Paper-and-pencil games
- Word games



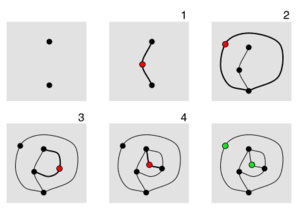 A 2-spot game of Sprouts. The game ends when the first player is unable to draw a connecting line between the only two free points, marked in green.
A 2-spot game of Sprouts. The game ends when the first player is unable to draw a connecting line between the only two free points, marked in green.Sprouts is a pencil-and-paper game with significant mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s.
The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules.
In so-called normal play, the player who makes the last move wins. In misère play, the player who makes the last move loses. (Misère Sprouts is perhaps the only misère combinatorial game that is played competitively in an organized forum.)
The diagram on the right shows a 2-spot game of normal-play Sprouts. After the fourth move, most of the spots are dead-they have three lines attached to them, so they cannot be used as endpoints for a new line. There are two spots (shown in green) that are still alive, having fewer than three lines attached. However, it is impossible to make another move, because a line from a live spot to itself would make four attachments, and a line from one live spot to the other would cross lines. Therefore, no fifth move is possible, and the first player loses. Live spots at the end of the game are called survivors and play a key role in the analysis of Sprouts.
It is not evident from the rules of Sprouts that the game always terminates, since the number of spots increase at each move. The correct approach is to consider the number of lives (opportunities to connect a line) instead of the number of spots. Then, we can show that if the game starts with n spots, it will end in no more than 3n−1 moves and no fewer than 2n moves.
In the following proofs, we suppose that a game starts with n spots and lasts for exactly m moves.
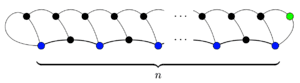 A game of sprouts with n initial spots (in blue) that ends in 3n−1 moves
A game of sprouts with n initial spots (in blue) that ends in 3n−1 movesEach spot starts with three lives and each move reduces the total number of lives in the game by one (two lives are lost at the ends of the line, but the new spot has one life). So at the end of the game there are 3n−m remaining lives. Each surviving spot has only one life (otherwise there would be another move joining that spot to itself), so there are exactly 3n−m survivors. There must be at least one survivor, namely the spot added in the final move. So 3n−m ≥ 1; hence a game can last no more than 3n−1 moves.
This upper bound is actually the maximum, and it can be attained in many ways by ensuring that there is only one survivor at the end of the game. For instance, the game on the right has one survivor and 3n−1 moves.
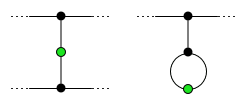 Live spots (green) and their dead neighbors (black).
Live spots (green) and their dead neighbors (black).At the end of the game each survivor has exactly two dead neighbors, in a technical sense of "neighbor", different from the ordinary graph notion of adjacency; see the diagram on the right. No dead spot can be the neighbor of two different survivors, for otherwise there would be a move joining the survivors. All other dead spots (not neighbors of a survivor) are called pharisees (from the Hebrew for "separated ones"). Suppose there are p pharisees. Then
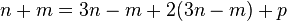
since initial spots + moves = total spots at end of game = survivors + neighbors + pharisees. Rearranging gives:
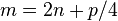
So a game lasts for at least 2n moves, and the number of pharisees is divisible by 4.
This lower bound on the length of a game is actually the minimum. The diagram on the right shows a completed game of 2n moves. It has n survivors, 2n neighbors and 0 pharisees.
Real games seem to turn into a battle over whether the number of moves will be k or k+1 (for some k, depending on the early moves in the game) with other possibilities being quite unlikely. One player tries to create enclosed regions containing survivors (thus reducing the total number of moves that will be played) and the other tries to create pharisees (thus increasing the number of moves that will be played).
Since Sprouts is a finite game where no draw is possible, a perfect strategy exists either for the first or the second player, depending on the number of initial spots. The main question about a given starting position is then to determine which player can force a win if he plays perfectly.
When the winning strategy is for the first player, it is said that the outcome of the position is a "win", and when the winning strategy is for the second player, it is said that the outcome of the position is a "loss" (because it is a loss from the point of view of the first player).
The outcome is determined by developing the game tree of the starting position. This can be done by hand only for a small number of spots, and all the new results since 1990 have been obtained by extensive search with computers.
Winning Ways for your Mathematical Plays reports that the 6-spot normal game was proved to be a win for the second player by Denis Mollison, with a hand-made analysis of 47 pages. It stood as the record for a long time, until the first computer analysis, which was done at Carnegie Mellon University, in 1990, by David Applegate, Guy Jacobson, and Daniel Sleator. They reached up to 11 spots with some of the best hardware available at the time.
Applegate, Jacobson and Sleator observed a pattern in their results, and conjectured that the first player has a winning strategy when the number of spots divided by six leaves a remainder of three, four, or five. This is a mathematical way of saying that the pattern displayed by the outcome in the table below repeats itself indefinitely, with a period of six spots.
| Spots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
| Normal Outcome | Loss | Loss | Win | Win | Win | Loss | Loss | Loss | Win | Win | Win | ... |
In 2001, Riccardo Focardi and Flamina Luccio described a method to prove by hand that the normal 7-spot game is a Loss.
Then, the computation results were extended in 2006 by Josh Jordan up to 14 spots. In 2007, Julien Lemoine and Simon Viennot introduced an algorithm based on the concept of nimbers to accelerate the computation, reaching up to 32 spots. They have extended the computation up to 44 spots in 2011, and three isolated starting positions, with 46, 47 and 53 spots.
The normal-play results so far are all consistent with the conjecture of Applegate, Jacobson and Sleator.
The computation history of the misère version of Sprouts is very similar to that of the normal version, with the same people involved. However, the misère version is more difficult to compute, and progress has been significantly slower.
In 1990, Applegate, Jacobson and Sleator reached up to nine spots. Based on their results, they conjectured that the outcome follows a regular pattern of period five. However, this conjecture was invalidated in 2007 when Josh Jordan and Roman Khorkov extended the misère analysis up to 12 spots : the 12-spot misère game is a win, and not the conjectured loss. The same team reached up to 16 spots in 2009. The same year, Julien Lemoine and Simon Viennot reached 17 spots with complicated algorithms. They were able to extend their analysis up to 20 points in 2011.
The results for misère play are now conjectured to follow a pattern of length six (with some exceptional values): the first player wins in misère Sprouts when the remainder (mod 6) is zero, four, or five, except that the first player wins the one-spot game and loses the four-spot game. The table below shows the pattern, with the two irregular values in bold.
| Spots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
| Misère Outcome | Win | Loss | Loss | Loss | Win | Win | Loss | Loss | Loss | Win | Win | Win | Loss | Loss | Loss | ... |
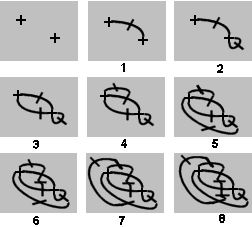 A 2-cross game of Brussels Sprouts lasting eight moves
A 2-cross game of Brussels Sprouts lasting eight movesA variant of the game, called Brussels Sprouts after the vegetable, starts with a number of crosses, i.e. spots with four free ends. Each move involves joining two free ends with a curve (again not crossing any existing line) and then putting a short stroke across the line to create two new free ends. This game is finite, and the total number of moves is predetermined by the initial number of crosses: the players cannot affect the result by their play.
Each move removes two free ends and introduces two more. With n initial crosses, the number of moves will be 5n−2, so a game starting with an odd number of crosses will be a first player win, while a game starting with an even number will be a second player win regardless of the moves.
To prove this (assuming that the game ends), let m denote the number of moves and v,e,f denote the number of vertices, edges, and faces of the planar graph obtained at the end of the game, respectively. We have:
The Euler characteristic for planar graphs is 2, so 2 = f-e+v = 4n-2m+n+m = 5n-m, hence m = 5n-2.