Longest uncrossed knight's path

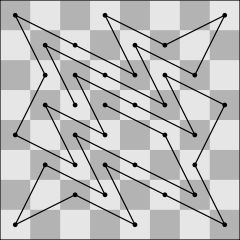
The longest uncrossed (or nonintersecting) knight's path is a mathematical problem involving a knight on the standard 8x8 chessboard or, more generally, on a square nxn board. The problem is to find the longest path the knight can take on the given board, such that the path does not intersect itself. A further distinction can be made between a closed path, which ends on the same field as where it begins, and an open path, which ends on a different field from where it begins.

Known solutions

The longest open paths are known only for n ≤ 9. Their lengths for n = 1, 2, …, 9 are:

0, 0, 2, 5, 10, 17, 24, 35, 47 (sequence A003192 in OEIS)

The longest closed paths are known only for n ≤ 10. Their lengths for n = 1, 2, …, 10 are:

0, 0, 0, 4, 8, 12, 24, 32, 42, 54 (sequence A157416 in OEIS)

The longest closed path for n = 7 of length 24.	The longest open path for n = 8 of length 35.

Generalizations

The problem can be further generalized to rectangular nxm boards, or even to boards in the shape of any polyomino. Other standard chess pieces than the knight are less interesting, but fairy chess pieces like the camel ((3,1)-leaper), giraffe ((4,1)-leaper) and zebra ((3,2)-leaper) lead to problems of comparable complexity.

Read more:

• A knight's tour is a self-intersecting knight's path visiting all fields of the board.
• TwixT, a board game based on uncrossed knight's paths.