

 A computer-generated image of a game of TwixT
A computer-generated image of a game of TwixTTwixT is a two-player strategy board game invented by Alex Randolph. It belongs to the connection family of games, along with Hex, Havannah, Y, PÜNCT and *Star. TwixT was short-listed for the first Spiel des Jahres in 1979, and was inducted into the Academy of Adventure Gaming Arts & Design's Hall of Fame, along with Randolph, in 2011.
3M originally published TwixT as part of its Bookshelf Games line, and Avalon Hill took over publication at a later date. The game is no longer produced in the United States, although Schmidt Spiele produced copies in Germany, and Kosmos published a version in 1998. Michael Katz, his nephew, owns the rights to Twixt since the death of Alex's widow, Gertrude Randolph.
Twixt is played on board comprising a 24x24 grid of holes, without the holes in the four corners. The rows at the four board edges are called "border rows". In the 3M edition, players are Red and Black; different sets may use different colors. The topmost and bottommost rows belong to the lighter color; the leftmost and rightmost rows to the darker color.
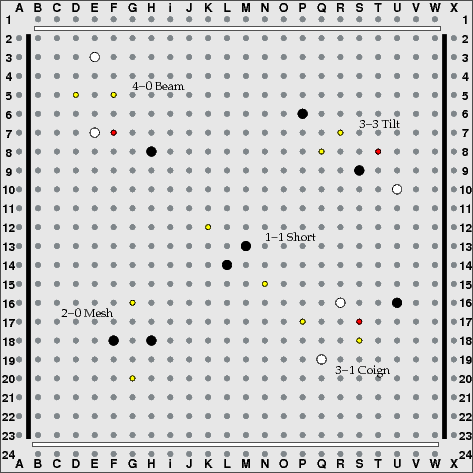
Despite such a large grid, games are frequently over before both sides have each made 25 moves. The tactics are very sharp and unforgiving. A knowledge of the most common peg patterns can help guide your eye towards the best move choices.
 The five setups.
The five setups.A setup is a pattern of two pegs of the same color which can connect to each other in a single move in two different ways. The gap between these pegs is generally difficult for the opponent to attack, since if one connection is blocked then the other is usually still available. There are five setups, each characterized by a name and by two numbers which represent the horizontal and vertical distances between these pegs. The larger value is listed first.
The yellow holes indicate where a third peg of the same color would form a double link connection. The red holes indicate possible points of attack for the opponent. For example, against white's beam setup in the top left, black could play at F7 which would link to H8. Placing a linked peg adjacent to a lone opposing peg this way is called a hammer attack. Black threatens to cut past E7 on one side or the other. In the top right, white could attack black's 3-3 tilt setup by linking to T8, threatening R9 or S10. Of course white would also be threatening in other directions, but our concern for the moment is just with setups and how to attack them. In the bottom right, black could launch a hammer attack with a link to S17, threatening Q16 or R15. Against the remaining two setups, the 2-0 mesh and the 1-1 short, a simple hammer attack will not work, because the two double linking paths are too widely separated. That does not mean that those setups are completely invulnerable, however.
There are plenty of other ways to place two pegs of the same color so that the gap between them is difficult to attack. The next diagram shows a few of them. The 5-2 gap is particularly strong. These two pegs can be connected in two moves in a variety of ways, usually too many for the opponent to block them all. The 5-0 gap is slightly more vulnerable. For example, if the O7 peg is unlinked, white might be able to attack at Q7. Then if black plays R6 threatening P5 or Q8, white could play O8, threatening N6 or R5.
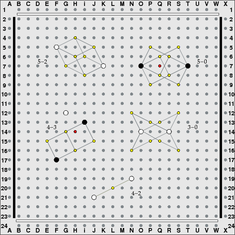
The 3-0 gap involves some very tricky tactics. For example, if black tries to attack with an unlinked peg at O15, white could respond with N16 which threatens to double link at P15.
The 4-2 gap is technically not a setup, because there is only one way to connect these pegs in one move. But without a nearby peg, it may be difficult for black to attack this pattern anyway. If black plays L20, white could respond at K20 or at M20, forming a combination of a coign setup and a short setup. Since the short setup is so difficult to attack, white will probably manage to connect J21 to N19, albeit in three moves rather than one. White might also respond to L20 with either K21 or M19, which is much more complicated.
It is usually good enough to play close to the peg you want to connect to, since the most important thing is to block your opponent. You'll probably be able to complete the connection later in the game. For example, in the 4-3 gap, if white attacks with H14 black might respond with H15, which is a 2-2 gap from F17. This is four knight's moves away, but physically the pegs are close. If white continues the attack with G16 then black has H16 which threatens to double link at J15.
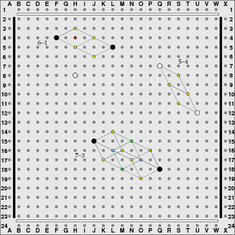
Here are a few more useful gaps to know. This is by no means an exhaustive list. The 6-1 gap can be vulnerable to attack like the 5-0 gap in the previous plate. With a white peg on H8 as shown, White could attack at H4, with the idea that black J4* would be answered by white F5*. In general, the "skinnier" the pattern of connecting holes is, such as with the 6-1 and 5-4 gaps, the more easily this gap could be attacked if the opponent has a peg close enough. But if there is no nearby opposing peg, such a pattern might be preferred because it crosses a large gap in few moves. An extreme example of this would be to extend a straight line of knight's moves by playing a 6-3 gap or 8-4 etc. If by making such a move you are also making another threat in another direction, this could be the most efficient possible use of the board. There are of course lots of gaps which would take three or more moves to connect. Shown here is the 7-3. Here black threatens to turn this into a "beam-tilt combination" by playing in either green hole (N15 or M18), or black might link to either blue hole (L16* or O17*) which would reduce this to a 5-2 gap.
The following diagrams use diagonal guide lines which emanate from the four corners of the common playing area. They are intended as a frame of reference on this huge grid of holes. They can help you see which side is going to win a corner battle.
The moves for each battle are numbered. One player makes the odd numbered moves, and the other player makes the even numbered moves. The notation shows an asterisk * for each link added to the peg that was just placed.
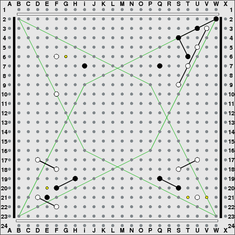
In the top left, black can hammer white with 1.G6*. If white responds with 2.D7* then after 3.E5* 4.C5* 5.C4* black has reached the crucial diagonal leading to B2. The top right shows the result of a similar fight with colors reversed, except here the hammer attack at T7 did not work because black was one row closer to the black border row, and black gained the crucial diagonal.
In a local battle, it is often a good idea to play where your opponent would like to play. In the bottom right, white has played 1.U21 which is a 2-1 block, or linking block, of the opponent and also forms a beam setup with U17. There are generally two ways to attack such a block, either a coign attack with 2.V21, or a short hammer attack with 2.T21. Neither attack works here. After 1.U21 2.V21 3.W20* 4.T22** 5.V22* white gains the corner. The bottom left is a mirror image, and shows the result after 1.D21 2.E21 3.F22* which threatens to cut through black's short setup with a double link at E20.
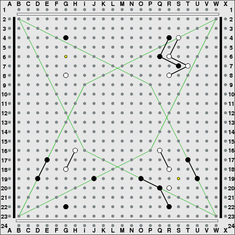
In the top left of this next diagram, white has another type of hammer attack. 1.G6 is called a mesh hammer. This works here because the white border row is so close that white can cut past black with either F4* or H4*, and also the 2-0 mesh setup between G6 and G8 is invulnerable to a simple hammer counterattack by black. The top right is a mirror image, and shows the result after 1.R6 2.Q6* 3.S4* 4.S7* 5.T7**.
The bottom left shows one way to defeat the mesh hammer attack. Black's "net" cannot be pierced by white in this instance. After 1.G20 2.H20** black threatens to cut through white's mesh setup with F19**. The bottom right is a mirror image which shows the point of black's defense.
Perhaps the best way to become familiar with tactics is to work through some puzzles. Many are available at in an interactive format. If you prefer not to allow Javascript, that same page has a link to download the puzzles, or most of the same puzzles are at
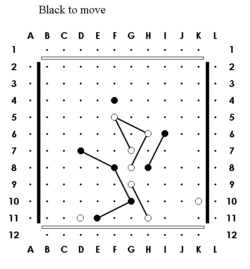
Perhaps the most popular variant is called Twixt PP where PP means paper and pencil. The rules are almost identical to standard TwixT. The only difference is with regard to link removal. When you play with paper and pencil, links are never removed, but your own links are allowed to cross each other. This means, for example, that a winning path might loop across itself. Crossed links are not inherently connected to each other. In other words, the object is still to form a sequence of pegs of your color, each directly linked to the next, which connects your border rows.
In terms of game outcome, for the vast majority of games, this rules change makes no difference. On the Little Golem turn-based server, thousands of games have been played, all using the PP ruleset. Of those, only a handful - less than 0.1% - can be pointed to as reasonably clear examples of games that probably would have ended differently under standard rules. Most of those are games which would have been a draw under standard rules instead of a win for one side. But one game almost certainly would have been a win for one side instead of the other.
A contrived example of such a situation on a smaller board is illustrated at the left. Under PP rules, black to move has an easy win with F9, linking to both E11 and H8. But under standard rules, black would have to first remove the F8/G10 link in order to place F9/H8, and that would allow white to then play at E9, double linking to D11 and G8. White is also threatening to play either i9, which is a triple link, or H10, which is unstoppably connected to the bottom. There is no way for black to effectively block all these threats.
Some players might argue that PP rules are cleaner than standard rules: for one thing, the incidence of draws is reduced. But draws are already quite rare under standard rules, and others believe the extra complications that result from link removal add depth and beauty to the game. In the Randolph series of puzzles, link removal is an essential part of several of those puzzles, and they would not be particularly interesting or challenging positions under PP rules.
Row handicapping is another variant which offers a way for players of different strengths to both enjoy a challenging game together. The simplest handicap is to eliminate the pie rule. Beyond that, one dimension of the grid is reduced. The weaker player moves first and also has less distance to cross. On a physical board, this might be implemented with two extra pieces of neutral color which look nothing like pegs but which fit in the holes. These are placed in the two new corners of the board, which are out of play, to indicate the new location of one of the weaker player's border rows. Six rows plus move might be a reasonable handicap between an experienced player and a beginner. The idea is to find a handicap where each player wins about half the time. Of course there is no pie rule for any handicap game.
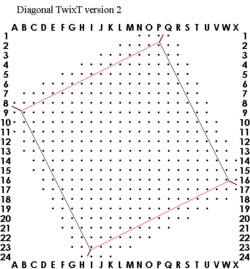
Different size grids from the standard 24x24 could be regarded as variants. The 12x12 board shown here leads to a very short game. It might be useful for development of computer programs which play the game, but between humans it is not very interesting. Even on the 24x24 grid, tactical considerations tend to predominate. The opening phase is over quickly, and the rest of the game is spent attempting to tactically justify the plan which you are now stuck with. By comparison, Hex, which has a very similar game object, may have more monotonous tactics, but strategical considerations are much more important. In this sense, Hex is more like Go than TwixT is, since a single move is generally less committal, and mistakes may not be punished as quickly. Since most commercial sets use boards which are made from four "quadrants" which either clip together or are hinged, a 36x36 grid could be cobbled together from three sets of the same size. In Europe, there briefly appeared a TwixT knock-off called "Imuri" which used a 30x30 grid. The board had no holes, and lines were drawn to indicate where the links could be placed. But the manufacturing quality was not so great; for example, link paths were drawn at each corner between adjacent border rows (A2 to C1 etc.) This edition was removed from shelves after Mr. Randolph threatened suit.
Mark Thompson's variant Diagonal TwixT has the same rules as standard TwixT, but the border lines no longer run parallel to the square grid of holes. Mark's idea was for border lines which run at a 45 degree angle to the grid. David Bush's version has the border lines running parallel to link paths. These variants result in many different tactical patterns. They feel like completely new games in this respect.
The official world championships were held as part of the Mind Sports Olympiad in 1997, 1998 and 1999. Since 2000 TwixT has still had a major international tournament as part of the MSO but there has been no official World Championships. In 2011, the MSO again called their TwixT event the World Championships and it was won by games all-rounder David Pearce.
TwixT has been proven to be PSPACE-complete for determining the game value, via a reduction from Hex. TwixT has also been shown to be NP-complete for whether a single set of vertices can support a connecting path, via a reduction from 3-SAT.
TwixT can be played online in an email version via . Twixt PP can be played at . It can be played on Scratch at .