
- Chess World Cup
- FIDE Grand Prix
- Olympiad
- World Championship
- List of strong tournaments
- List of world championships

- Checkmate patterns
- Chess openings
- Chess strategy
- Chess tactics
- Chess theory
- Endgames
- Pawn structure
- Problems/Compositions












| a | b | c | d | e | f | g | h | ||
| 8 |

   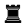      |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
The GBR code (or Guy-Blandford-Roycroft code) is a system of representing the position of chess pieces on a chessboard. Publications such as EG use it to classify endgame types and to index endgame studies.
The code is named after Richard Guy, Hugh Blandford and John Roycroft. The first two devised the original system (the Guy-Blandford code) using different figures to represent the number of pieces. Roycroft suggested to count one for a white piece and three for a black piece in order to make the code easier to memorise.
In the GBR code, every chess position is represented by six digits, in the following format:
abcd.ef
For the first four digits, each white piece counts as 1, and each black piece counts as 3. Thus, for example, if White has two knights and Black has one knight, numeral d = 1 + 1 + 3 = 5. If that is all the material other than the kings, the position is classified 0005. Values 0 through 8 represent all normal permutations of force; 9 is used if either side has promoted material.
The last two digits of the code represent the number of white and black pawns, respectively.
GBR code can be used to refer to a general class of material. For example, the endgame of two knights against pawn (as famously analysed by A.A. Troitzky, leading to his discovery of the Troitzky line), is GBR class 0002.01.
When indexing or referring to specific positions, rather than generalised material imbalances, the code may be extended in various ways. Two common ones are to prefix "+" to indicate the stipulation "White to play and win" or "=" for "White to play and draw"; and to suffix the position of the white and black kings. With these additions, the position to the right, a draw study by Leonid Kubbel (First Prize, Shakhmaty, 1925), is classified as =0323.12g3g1. (The solution is: 1.Bf2+ Kh1 2.h7 c2+ 3.Be3 Rxe3+ 4.Kf2 Rh3 5.Bd5+ cxd5 6.hxg8=Q Rh2+ 7.Kf3 c1=Q 8.Qg2+ Rxg2.) The positions of other pieces can also be added; this produces a notation that provides the same information as Forsyth-Edwards Notation.
| White material | Black material | GBR class |
|---|---|---|
| KQ | K | 1000 |
| KR | K | 0100 |
| KB | K | 0010 |
| KN | K | 0001 |
| KNN | K | 0002 |
| K | KN | 0003 |
| KN | KN | 0004 |
| KNN | KN | 0005 |
| K | KNN | 0006 |
| KN | KNN | 0007 |
| KNN | KNN | 0008 |
| KNNN | KNN | 0009 |
| KPPP | KPP | 0000.32 |
| KNN | KP | 0002.01 |
| KBB | KN | 0023 |
| KQ | KR | 1300 |
| KQP | KQ | 4000.10 |
| KRP | KR | 0400.10 |
| KRRP | KRR | 0800.10 |
| KBBP | KNN | 0026.10 |
| KBBP | KRNPP | 0323.12 |