



The first moves of a backgammon game are the opening moves, collectively referred to as the opening, and studied in the backgammon opening theory. Backgammon opening theory is not developed in as much detail as opening theory in chess, which has been widely studied. The reason for this is that following the first move in backgammon, there are 21 dice roll outcomes on each subsequent move, and many alternative plays for each outcome, making the tree of possible positions in backgammon expand much more rapidly than in chess.
Despite the complications posed by this rapid branching of possibilities, over the course of many years, a consensus did develop amongst backgammon experts on what is the preferred opening move for each given roll. Following the emergence of self-trained backgammon-playing neural networks, the insights on what are the best opening moves have changed in some unexpected ways.
The table below summarises the most commonly preferred moves, for each of the 15 possible opening rolls, as selected by detailed computer simulations, referred to as "rollouts". There are no opening moves consisting of doubles, because at the start of the game, each player rolls one die. Whoever rolls higher moves first, using the numbers on the already-rolled dice. In the case of a tie, the players roll again. In cases where no preferred play but only two or more alternative plays are given, these appear to be of equivalent strength within the statistical uncertainties of the simulations and no play could be singled out that is clearly superior.
The moves are captured in standard backgammon notation. For instance, 8/5 denotes the move of a piece from the 8-point to the 5-point.
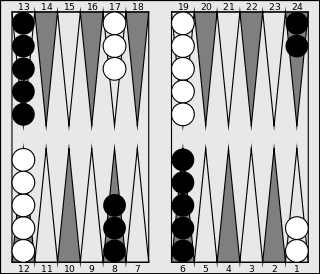 Backgammon opening position, board points numbered to register the movements of the black checkers
Backgammon opening position, board points numbered to register the movements of the black checkers| Roll | Preferred play | Common alternatives | ||
|---|---|---|---|---|
| 2-1 | 13/11, 6/5 | 24/23, 13/11 | - | |
| 3-1 | 8/5, 6/5 | - | - | |
| 4-1 | 24/23, 13/9 | 13/9, 6/5 | - | |
| 5-1 | 24/23, 13/8 | 13/8, 6/5 | - | |
| 6-1 | 13/7, 8/7 | - | - | |
| 3-2 | 24/21, 13/11 | 13/11, 13/10 | - | |
| 4-2 | 8/4, 6/4 | - | - | |
| 5-2 | 24/22, 13/8 | 13/11, 13/8 | - | |
| 6-2 | 24/18, 13/11 | 13/5 | - | |
| 4-3 | 13/10, 13/9 | 24/21, 13/9 | 24/20, 13/10 | |
| 5-3 | 8/3, 6/3 | - | - | |
| 6-3 | 24/18, 13/10 | 24/15 | - | |
| 5-4 | 24/20, 13/8 | 13/9, 13/8 | 24/15 | |
| 6-4 | 24/18, 13/9 | 8/2, 6/2 | 24/14 | |
| 6-5 | 24/13 | - | - | |
The general message that emerges from the above table can be summarised as follows: unless one can make a point, and with the exception of the running move 24/13 (in which, having thrown a 6-5, the player moves a piece from the 24-point to the 13-point; the lover's leap), a successful play is often the combination of splitting the 24-point and moving a checker from the 13-point. The latter move should be as small as possible (resulting in a builder close to the 13-point), unless the stack at the 8-point can be reached (resulting in an equal distribution between the 13-point and the 8-point). However, there are plenty of exceptions to this rule; for example, a 4-3 or 3-2 is often best played by moving two checkers from the 13 point.
The above opening moves which emerged from computer analysis demonstrate that a number of opening moves that were unquestioned for many decades are now considered suboptimal. One example is the move 13/11-13/8 on the roll 5-2. Although not a bad move, the alternative choice preferred by the analyses, 24/22-13/8, is now generally agreed upon to be optimal. In other cases, computer analysis has resulted in alternative strategies that were not seriously considered in the past. For instance, the opening move 8/2-6/2 for a roll of 6-4 was in the past greeted with disdain from experts (making the 2-point instead of trying for a higher home point), but turns out to be on average as effective as the usual plays (24/14 and 24/18-13/9).
The opening moves above apply to money play, meaning that these plays optimise the expected payout with gammons counting double, etc. In match play the match score affects the checker play and one of the alternative plays may come out on top in computer simulations depending on the score. In a "Gammon-go" situation the player does not care about whether they lose a single game or a gammon, but they have much to gain from winning a gammon; thus they can benefit from aggressive openings. The opposite may be true in "gammon-save" situations, where the player has little to lose from losing a single game, but much to lose from losing a gammon. At double-match-point (DMP) where the score is tied with each player needing one point to win, gammons do not matter for either player.
In practice, an even more important influencing factor is the preferred style of the player. A player might have a strong preference for one out of a number of alternative opening plays that are on average as effective, because the character of the move (passive or aggressive) better suits his or her playing style.