
- Chess World Cup
- FIDE Grand Prix
- Olympiad
- World Championship
- List of strong tournaments
- List of world championships

- Checkmate patterns
- Chess openings
- Chess strategy
- Chess tactics
- Chess theory
- Endgames
- Pawn structure
- Problems/Compositions












In chess, a grotesque is a problem or endgame study which features a particularly unlikely initial position, especially one in which White fights with a very small force against a much larger black army. Grotesques are generally intended to be humorous.
| a | b | c | d | e | f | g | h | ||
| 8 |

    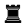      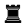        |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
A particularly extreme example by Ottó Bláthy is illustrated in the diagram to the left. In the initial position Black has all sixteen pieces remaining and White has just a single pawn on its starting square, yet it is White who will deliver checkmate.
This position in Forsyth-Edwards Notation (FEN) is : 8/8/8/2p5/1pp5/brpp4/qpprpK1P/1nkbn3 w - - 0 1
The solution is:
The fact that the black queen must be on a1 rather than a2 when White plays Nxb3 explains why 2.h4 does not work. Similarly, if the white knight takes a more direct route to the b3 square with 8.Ng6 Qa2 9.Ne5 Qa1 10.Nxc4 Qa2 11.Na5, Black can lose a move with 11...c4! 12.Nxc4 Qa1 13.Na5 Qa2 and there is no mate. This kind of precise timing is quite a common feature in this type of problem.
Tigran Gorgiev| a | b | c | d | e | f | g | h | ||
| 8 |

            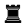  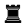   |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
The composer most closely associated with the grotesque is probably Tigran Gorgiev; one of his examples is shown to the right.
This position in Forsyth-Edwards Notation (FEN) is : 8/8/4N3/4Q3/1pp5/1p3N2/bpqp1p2/nrkrbK2 w - - 0 1
This time, White is to play and draw. This is achieved by sacrificing most of his already small force to compel Black to repeat moves: 1.Nf4 Qd3+ (otherwise 2.Ne2+ leads to mate) 2.Nxd3+ cxd3 3.Qc3+ bxc3 4.Ne5 Kc2 5.Nc4 Kc1 6.Ne5 and Black has nothing more than a draw by repetition. Note that only the squares c4 and e5 will do for the white knight; if, for example 4.Nd4 then 4...Nc2 allows Black to free himself (this is not possible with the knight on e5 because of Nxd3#); and if, for example, 5.Nc6 then Black can free himself with 5...Rbc1 or 5...Rdc1 (not possible with the knight on c4 because of Na3# and Ne3# respectively).
| a | b | c | d | e | f | g | h | ||
| 8 |

                       |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Similar play to that found in grotesques such as these may also be found in very long moremovers (problems with the stipulation "White to play and checkmate Black in no more than n moves", where n is very high, sometimes over 100, known as longmovers), of which Ottó Bláthy was also a notable composer.
To the right is a kind of problem quite closely related to these kinds of grotesques: this time it is White who has a clear material advantage, but it is difficult to make anything of it because of the locked pawn chain.
This position in Forsyth-Edwards Notation (FEN) is : 8/8/8/1k3p2/p1p1pPp1/PpPpP1Pp/1P1P3P/QNK2NRR w - - 0 1
At first glance it seems there is nothing to be done - on moves like Rg2, White cannot make progress unless Black captures - but White does have one plan: to play Qa2 at an appropriate moment in order to threaten Qxb3. Doing this immediately does not work (Black simply promotes on a1 and it is Black who wins by ... Qa2-b3-c2 mate), but there is a way: