Bridge probabilities
In the game of bridge mathematical probabilities play a significant role. Different declarer play strategies lead to success depending on the distribution of opponent's cards. To decide which strategy has highest likelihood of success, the declarer needs to have at least an elementary knowledge of probabilities.
The tables below specify the various prior probabilities, i.e. the probabilities in the absence of any further information. During bidding and play, more information about the hands becomes available, allowing players to improve their probability estimates.
Probability of suit distributions in two hidden hands
This table represents the different ways that two to thirteen particular cards may be distributed, or may lie or split, between two unknown 13-card hands (before the bidding and play, or a priori).
The table also shows the number of combinations of particular cards that match any numerical split and the probabilities for each combination.
These probabilities follow directly from the law of Vacant Places.
Number
of Cards |
Distribution |
Probability |
Combinations |
Individual
Probability |
| 2 |
1 - 1 |
0.52 |
2 |
0.26 |
| 2 - 0 |
0.48 |
2 |
0.24 |
| 3 |
2 - 1 |
0.78 |
6 |
0.13 |
| 3 - 0 |
0.22 |
2 |
0.11 |
| 4 |
2 - 2 |
0.41 |
6 |
0.0678~ |
| 3 - 1 |
0.50 |
8 |
0.0622~ |
| 4 - 0 |
0.10 |
2 |
0.0478~ |
| 5 |
3 - 2 |
0.68 |
20 |
0.0339~ |
| 4 - 1 |
0.28 |
10 |
0.02826~ |
| 5 - 0 |
0.04 |
2 |
0.01956~ |
| 6 |
3 - 3 |
0.36 |
20 |
0.01776~ |
| 4 - 2 |
0.48 |
30 |
0.01615~ |
| 5 - 1 |
0.15 |
12 |
0.01211~ |
| 6 - 0 |
0.01 |
2 |
0.00745~ |
| 7 |
4 - 3 |
0.62 |
70 |
0.00888~ |
| 5 - 2 |
0.31 |
42 |
0.00727~ |
| 6 - 1 |
0.07 |
14 |
0.00484~ |
| 7 - 0 |
0.01 |
2 |
0.00261~ |
| 8 |
4 - 4 |
0.33 |
70 |
0.00467~ |
| 5 - 3 |
0.47 |
112 |
0.00421~ |
| 6 - 2 |
0.17 |
56 |
0.00306~ |
| 7 - 1 |
0.03 |
16 |
0.00178~ |
| 8 - 0 |
0.00 |
2 |
0.00082~ |
Probability of HCP distribution
High card points (HCP) are usually counted using the Milton Work scale of 4/3/2/1 points for each Ace/King/Queen/Jack respectively. The a priori probabilities that a given hand contains no more than a specified number of HCP is given in the table below. To find the likelihood of a certain point range, one simply subtracts the two relevant cumulative probabilities. So, the likelihood of being dealt a 12-19 HCP hand (ranges inclusive) is the probability of having at most 19 HCP minus the probability of having at most 11 HCP, or: 0.986 − 0.652 = 0.334.
| HCP |
Probability |
|
HCP |
Probability |
|
HCP |
Probability |
|
HCP |
Probability |
|
HCP |
Probability |
| 0 |
0.0036 |
8 |
0.3748 |
16 |
0.9355 |
24 |
0.9995 |
32 |
1.0000 |
| 1 |
0.0115 |
9 |
0.4683 |
17 |
0.9591 |
25 |
0.9998 |
33 |
1.0000 |
| 2 |
0.0251 |
10 |
0.5624 |
18 |
0.9752 |
26 |
0.9999 |
34 |
1.0000 |
| 3 |
0.0497 |
11 |
0.6518 |
19 |
0.9855 |
27 |
1.0000 |
35 |
1.0000 |
| 4 |
0.0882 |
12 |
0.7321 |
20 |
0.9920 |
28 |
1.0000 |
36 |
1.0000 |
| 5 |
0.1400 |
13 |
0.8012 |
21 |
0.9958 |
29 |
1.0000 |
37 |
1.0000 |
| 6 |
0.2056 |
14 |
0.8582 |
22 |
0.9979 |
30 |
1.0000 |
| 7 |
0.2858 |
15 |
0.9024 |
23 |
0.9990 |
31 |
1.0000 |
Hand pattern probabilities
A hand pattern denotes the distribution of the thirteen cards in a hand over the four suits. In total 39 hand patterns are possible, but only 13 of them have an a priori probability exceeding 1%. The most likely pattern is the 4-4-3-2 pattern consisting of two four-card suits, a three-card suit and a doubleton.
Note that the hand pattern leaves unspecified which particular suits contain the indicated lengths. For a 4-4-3-2 pattern, one needs to specify which suit contains the three-card and which suit contains the doubleton in order to identify the length in each of the four suits. There are four possibilities to first identify the three-card suit and three possibilities to next identify the doubleton. Hence, the number of suit permutations of the 4-4-3-2 pattern is twelve. Or, stated differently, in total there are twelve ways a 4-4-3-2 pattern can be mapped onto the four suits.
Below table lists all 39 possible hand patterns, their probability of occurrence, as well as the number of suit permutations for each pattern. The list is ordered according to likelihood of occurrence of the hand patterns.
| Pattern |
Probability |
# |
| 4-4-3-2 |
0.2155 |
12 |
| 5-3-3-2 |
0.1552 |
12 |
| 5-4-3-1 |
0.1293 |
24 |
| 5-4-2-2 |
0.1058 |
12 |
| 4-3-3-3 |
0.1054 |
4 |
| 6-3-2-2 |
0.0564 |
12 |
| 6-4-2-1 |
0.0470 |
24 |
| 6-3-3-1 |
0.0345 |
12 |
| 5-5-2-1 |
0.0317 |
12 |
| 4-4-4-1 |
0.0299 |
4 |
| 7-3-2-1 |
0.0188 |
24 |
| 6-4-3-0 |
0.0133 |
24 |
| 5-4-4-0 |
0.0124 |
12 |
|
| Pattern |
Probability |
# |
| 5-5-3-0 |
0.0090 |
12 |
| 6-5-1-1 |
0.0071 |
12 |
| 6-5-2-0 |
0.0065 |
24 |
| 7-2-2-2 |
0.0051 |
4 |
| 7-4-1-1 |
0.0039 |
12 |
| 7-4-2-0 |
0.0036 |
24 |
| 7-3-3-0 |
0.0027 |
12 |
| 8-2-2-1 |
0.0019 |
12 |
| 8-3-1-1 |
0.0012 |
12 |
| 7-5-1-0 |
0.0011 |
24 |
| 8-3-2-0 |
0.0011 |
24 |
| 6-6-1-0 |
0.00072 |
12 |
| 8-4-1-0 |
0.00045 |
24 |
|
| Pattern |
Probability |
# |
| 9-2-1-1 |
0.00018 |
12 |
| 9-3-1-0 |
0.00010 |
24 |
| 9-2-2-0 |
0.000082 |
12 |
| 7-6-0-0 |
0.000056 |
12 |
| 8-5-0-0 |
0.000031 |
12 |
| 10-2-1-0 |
0.000011 |
24 |
| 9-4-0-0 |
0.000010 |
12 |
| 10-1-1-1 |
0.000004 |
4 |
| 10-3-0-0 |
0.0000015 |
12 |
| 11-1-1-0 |
0.0000002 |
12 |
| 11-2-0-0 |
0.0000001 |
12 |
| 12-1-0-0 |
0.000000003 |
12 |
| 13-0-0-0 |
0.000000000006 |
4 |
|
|
The 39 hand patterns can by classified into four hand types: balanced hands, three-suiters, two suiters and single suiters. Below table gives the a priori likelihoods of being dealt a certain hand-type.
| Hand type |
Patterns |
Probability |
| Balanced |
4-3-3-3, 4-4-3-2, 5-3-3-2 |
0.4761 |
| Two-suiter |
5-4-2-2, 5-4-3-1, 5-5-2-1, 5-5-3-0, 6-5-1-1, 6-5-2-0, 6-6-1-0, 7-6-0-0 |
0.2902 |
| Single-suiter |
6-3-2-2, 6-3-3-1, 6-4-2-1, 6-4-3-0, 7-2-2-2, 7-3-2-1, 7-3-3-0, 7-4-1-1, 7-4-2-0, 7-5-1-0, 8-2-2-1, 8-3-1-1, 8-3-2-0, 8-4-1-0, 8-5-0-0, 9-2-1-1, 9-2-2-0, 9-3-1-0, 9-4-0-0, 10-1-1-1, 10-2-1-0, 10-3-0-0, 11-1-1-0, 11-2-0-0, 12-1-0-0, 13-0-0-0 |
0.1915 |
| Three-suiter |
4-4-4-1, 5-4-4-0 |
0.0423 |
Alternative grouping of the 39 hand patterns can be made either by longest suit or by shortest suit. Below tables gives the a priori chance of being dealt a hand with a longest or a shortest suit of given length.
| Longest suit |
Patterns |
Probability |
| 4 card |
4-3-3-3, 4-4-3-2, 4-4-4-1 |
0.3508 |
| 5 card |
5-3-3-2, 5-4-2-2, 5-4-3-1, 5-5-2-1, 5-4-4-0, 5-5-3-0 |
0.4434 |
| 6 card |
6-3-2-2, 6-3-3-1, 6-4-2-1, 6-4-3-0, 6-5-1-1, 6-5-2-0, 6-6-1-0 |
0.1655 |
| 7 card |
7-2-2-2, 7-3-2-1, 7-3-3-0, 7-4-1-1, 7-4-2-0, 7-5-1-0, 7-6-0-0 |
0.0353 |
| 8 card |
8-2-2-1, 8-3-1-1, 8-3-2-0, 8-4-1-0, 8-5-0-0 |
0.0047 |
| 9 card |
9-2-1-1, 9-2-2-0, 9-3-1-0, 9-4-0-0 |
0.00037 |
| 10 card |
10-1-1-1, 10-2-1-0, 10-3-0-0 |
0.000017 |
| 11 card |
11-1-1-0, 11-2-0-0 |
0.0000003 |
| 12 card |
12-1-0-0 |
0.000000003 |
| 13 card |
13-0-0-0 |
0.000000000006 |
| Shortest suit |
Patterns |
Probability |
| Three card |
4-3-3-3 |
0.1054 |
| Doubleton |
4-4-3-2, 5-3-3-2, 5-4-2-2, 6-3-2-2, 7-2-2-2 |
0.5380 |
| Singleton |
4-4-4-1, 5-4-3-1, 5-5-2-1, 6-3-3-1, 6-4-2-1, 6-5-1-1, 7-3-2-1, 7-4-1-1, 8-2-2-1, 8-3-1-1, 9-2-1-1, 10-1-1-1 |
0.3055 |
| Void |
5-4-4-0, 5-5-3-0, 6-4-3-0, 6-5-2-0, 6-6-1-0, 7-3-3-0, 7-4-2-0, 7-5-1-0, 7-6-0-0, 8-3-2-0, 8-4-1-0, 8-5-0-0, 9-2-2-0, 9-3-1-0, 9-4-0-0, 10-2-1-0, 10-3-0-0, 11-1-1-0, 11-2-0-0, 12-1-0-0, 13-0-0-0 |
0.0512 |
Number of possible deals
In total there are 53,644,737,765,488,792,839,237,440,000 (5.36 x 1028) different deals possible, which is equal to 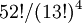 . The immenseness of this number can be understood by answering the question "How large an area would you need to spread all possible bridge deals if each deal would occupy only one square millimeter?". The answer is: an area more than a hundred million times the surface area of Earth.
. The immenseness of this number can be understood by answering the question "How large an area would you need to spread all possible bridge deals if each deal would occupy only one square millimeter?". The answer is: an area more than a hundred million times the surface area of Earth.
Obviously, the deals that are identical except for swapping - say - the ♥2 and the ♥3 would be unlikely to give a different result. To make the irrelevance of small cards explicit (which is not always the case though), in bridge such small cards are generally denoted by an 'x'. Thus, the "number of possible deals" in this sense depends of how many non-honour cards (2, 3, .. 9) are considered 'indistinguishable'. For example, if 'x' notation is applied to all cards smaller than ten, then the suit distributions A987-K106-Q54-J32 and A432-K105-Q76-J98 would be considered identical.
The table below gives the number of deals when various numbers of small cards are considered indistinguishable.
| Suit composition |
Number of deals |
| AKQJT9876543x |
53,644,737,765,488,792,839,237,440,000 |
| AKQJT987654xx |
7,811,544,503,918,790,990,995,915,520 |
| AKQJT98765xxx |
445,905,120,201,773,774,566,940,160 |
| AKQJT9876xxxx |
14,369,217,850,047,151,709,620,800 |
| AKQJT987xxxxx |
314,174,475,847,313,213,527,680 |
| AKQJT98xxxxxx |
5,197,480,921,767,366,548,160 |
| AKQJT9xxxxxxx |
69,848,690,581,204,198,656 |
| AKQJTxxxxxxxx |
800,827,437,699,287,808 |
| AKQJxxxxxxxxx |
8,110,864,720,503,360 |
| AKQxxxxxxxxxx |
74,424,657,938,928 |
| AKxxxxxxxxxxx |
630,343,600,320 |
| Axxxxxxxxxxxx |
4,997,094,488 |
| xxxxxxxxxxxxx |
37,478,624 |
Note that the last entry in the table (37,478,624) corresponds to the number of different distributions of the deck (the number of deals when cards are only distinguished by their suit).
Probability of Losing-Trick Counts
The Losing-Trick Count is an alternative to the HCP count as a method of hand evaluation.
| LTC |
Number of Hands |
Probability |
| 0 |
4,245,032 |
0.000668% |
| 1 |
90,206,044 |
0.0142% |
| 2 |
872,361,936 |
0.137% |
| 3 |
5,080,948,428 |
0.8% |
| 4 |
19,749,204,780 |
3.11% |
| 5 |
53,704,810,560 |
8.46% |
| 6 |
104,416,332,340 |
16.4% |
| 7 |
145,971,648,360 |
23.0% |
| 8 |
145,394,132,760 |
22.9% |
| 9 |
100,454,895,360 |
15.8% |
| 10 |
45,618,822,000 |
7.18% |
| 11 |
12,204,432,000 |
1.92% |
| 12 |
1,451,520,000 |
0.229% |
| 13 |
0 |
0% |
COMMENTS



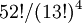 . The immenseness of this number can be understood by answering the question "How large an area would you need to spread all possible bridge deals if each deal would occupy only one square millimeter?". The answer is: an area more than a hundred million times the surface area of Earth.
. The immenseness of this number can be understood by answering the question "How large an area would you need to spread all possible bridge deals if each deal would occupy only one square millimeter?". The answer is: an area more than a hundred million times the surface area of Earth.