- Chess problem
- Chess puzzle
- Eight queens puzzle
- KenKen
- Mahjong solitaire
- Peg solitaire
- Pentomino
- Prisoners and hats puzzle
- Rubik's Cube
- Tangram
- Three cups problem
- Tiling puzzle
- Tsumego
- Tsumeshogi
Comparison of labeling schemes for the 12 possible pentomino shapes. The first naming convention is the one used in this article. The second method is Conway's.A pentomino is a plane geometric figure formed by joining five equal squares edge to edge. It is a polyomino with five cells. There are twelve pentominoes, not counting rotations and reflections as distinct. They are used chiefly in recreational mathematics for puzzles and problems. Pentominoes were formally defined by American professor Solomon W. Golomb starting in 1953 and later in his 1965 book Polyominoes: Puzzles, Patterns, Problems, and Packings. Golomb coined the term "pentomino" from the Ancient Greek πέντε / pénte, "five", and the -omino of domino, fancifully interpreting the "d-" of "domino" as if it were a form of the Greek prefix "di-" (two). Golomb named the 12 free pentominoes after letters of the Latin alphabet that they resemble.
Ordinarily, the pentomino obtained by reflecting or rotating a pentomino does not count as a different pentomino. The F, L, N, P, Y, and Z pentominoes are chiral; adding their reflections (F', J, N', Q, Y', S) brings the number of one-sided pentominoes to 18. Pentominoes I, T, U, V, W, and X, remain the same when reflected. This matters in some video games in which the pieces may not be reflected, such as Tetris imitations and Rampart.
Each of the twelve pentominoes satisfies the Conway criterion; hence every pentomino is capable of tiling the plane. Each chiral pentomino can tile the plane without reflecting it.
John Horton Conway proposed an alternate labeling scheme for pentominoes, using O instead of I, Q instead of L, R instead of F, and S instead of N. The resemblance to the letters is more strained, especially for the O pentomino, but this scheme has the advantage of using 12 consecutive letters of the alphabet. It is used by convention in discussing Conway's Game of Life, where, for example, one speaks of the R-pentomino instead of the F-pentomino.
The 12 pentominoes can form 18 different shapes, with 6 being mirroredPentominoes have the following categories of symmetry:
If reflections of a pentomino are considered distinct, as they are with one-sided pentominoes, then the first and fourth categories above double in size, resulting in an extra 6 pentominoes for a total of 18. If rotations are also considered distinct, then the pentominoes from the first category count eightfold, the ones from the next three categories (T, U, V, W, Z) count fourfold, I counts twice, and X counts only once. This results in 5x8 + 5x4 + 2 + 1 = 63 fixed pentominoes.
For example, the eight possible orientations of the L, F, N, P, and Y pentominoes are as follows:
For 2D figures in general there are two more categories:
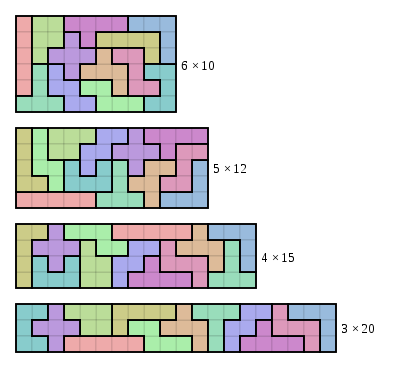
A standard pentomino puzzle is to tile a rectangular box with the pentominoes, i.e. cover it without overlap and without gaps. Each of the 12 pentominoes has an area of 5 unit squares, so the box must have an area of 60 units. Possible sizes are 6x10, 5x12, 4x15 and 3x20. The avid puzzler can probably solve these problems by hand within a few hours. A more challenging task, typically requiring a computer search, is to count the total number of solutions in each case.
The 6x10 case was first solved in 1960 by Colin Brian and Jenifer Haselgrove. There are exactly 2339 solutions, excluding trivial variations obtained by rotation and reflection of the whole rectangle, but including rotation and reflection of a subset of pentominoes (which sometimes provides an additional solution in a simple way). The 5x12 box has 1010 solutions, the 4x15 box has 368 solutions, and the 3x20 box has just 2 solutions (one is shown in the figure, and the other one can be obtained from the solution shown by rotating, as a whole, the block consisting of the L, N, F, T, W, Y, and Z pentominoes).
A somewhat easier (more symmetrical) puzzle, the 8x8 rectangle with a 2x2 hole in the center, was solved by Dana Scott as far back as 1958. There are 65 solutions. Scott's algorithm was one of the first applications of a backtracking computer program. Variations of this puzzle allow the four holes to be placed in any position. One of the external links uses this rule. Most such patterns are solvable, with the exceptions of placing each pair of holes near two corners of the board in such a way that both corners could only be fitted by a P-pentomino, or forcing a T-pentomino or U-pentomino in a corner such that another hole is created.
Efficient algorithms have been described to solve such problems, for instance by Donald Knuth. Running on modern hardware, these pentomino puzzles can now be solved in mere seconds.
A pentacube is a polycube of five cubes. Twelve of the 29 pentacubes correspond to the twelve pentominoes extruded to a depth of one square. A pentacube puzzle or 3D pentomino puzzle, amounts to filling a 3-dimensional box with these 1-layer pentacubes, i.e. cover it without overlap and without gaps. Each of the 12 pentacubes consists of 5 unit cubes, and are like 2D pentominoes but with unit thickness. Clearly the box must have a volume of 60 units. Possible sizes are 2x3x10 (12 solutions), 2x5x6 (264 solutions) and 3x4x5 (3940 solutions). Following are one solution of each case.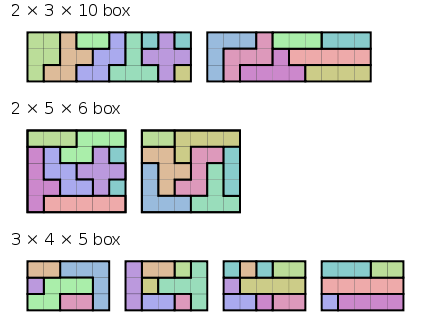 
Alternatively one could also consider combinations of five cubes that are themselves 3D, i.e., are not part of one layer of cubes. However, in addition to the 12 extruded pentominoes, 6 sets of chiral pairs and 5 pieces make total 29 pieces, resulting 145 cubes, which will not make a 3D box.
There are board games of skill based entirely on pentominoes. Such games are often simply called "Pentominoes".
One of the games is played on an 8x8 grid by two or three players. Players take turns in placing pentominoes on the board so that they do not overlap with existing tiles and no tile is used more than once. The objective is to be the last player to place a tile on the board. This version of Pentominoes is called "Golomb's Game".
The two-player version has been weakly solved in 1996 by Hilarie Orman. It was proved to be a first-player win by examining around 22 billion board positions.
Pentominoes, and similar shapes, are also the basis of a number of other tiling games, patterns and puzzles. For example, the French board game Blokus is played with 4 opposing color sets of polyominoes. In Blokus, each color begins with every pentomino (12), as well as every tetromino (5), every triomino (2), every domino (1), and the monomino (1). Like the game Pentominoes, the goal is to use all of your tiles, and a bonus is given if the monomino is played on the very last move. The player with the fewest blocks remaining wins.
The game of Cathedral is also based on polyominoes.
Parker Brothers released a multi-player pentomino board game called Universe in 1966. Its theme is based on an outtake from the movie 2001: A Space Odyssey in which the astronaut (seen playing chess in the final version) is playing a two-player pentomino game against a computer. The front of the board game box features scenes from the movie as well as a caption describing it as the "game of the future". The game comes with 4 sets of pentominoes in red, yellow, blue, and white. The board has two playable areas: a base 10x10 area for two players with an additional 25 squares (two more rows of 10 and one offset row of 5) on each side for more than two players.
Game manufacturer Lonpos has a number of games that use the same pentominoes, but on different game planes. Their 101 Game has a 5 x 11 plane. By changing the shape of the plane, thousands of puzzles can be played, although only a relatively small selection of these puzzles are available in print.
The first pentomino problem, written by Henry Dudeney, was published in 1907 in the Canterbury Puzzles.
Pentominoes were featured in a prominent subplot of Arthur C. Clarke's novel Imperial Earth, published in 1975. Clarke also wrote an essay in which he described the game and how he got hooked on it.
They were also featured in Blue Balliett's Chasing Vermeer, which was published in 2003 and illustrated by Brett Helquist, as well as its sequels, The Wright 3 and The Calder Game.
In the New York Times crossword puzzle for June 27, 2012, the clue for an 11-letter word at 37 across was "Complete set of 12 shapes formed by this puzzle's black squares."