Nonomino

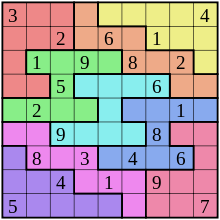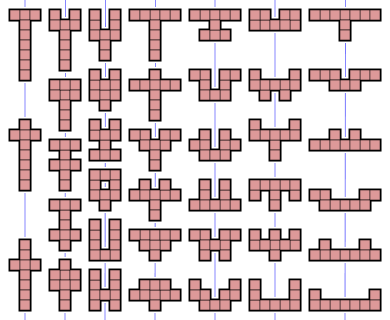
A nonomino or Jigsaw Sudoku puzzle, as seen in the Sunday Telegraph

A nonomino (or 9-omino) is a polyomino of order 9, that is, a polygon in the plane made of 9 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix non(a)-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free nonominoes. When reflections are considered distinct, there are 2,500 one-sided nonominoes. When rotations are also considered distinct, there are 9,910 fixed nonominoes.

Symmetry

The 1,285 free nonominoes can be classified according to their symmetry groups:

• 1,196 nonominoes have no symmetry. Their symmetry group consists only of the identity mapping.
• 38 nonominoes have an axis of reflection symmetry aligned with the gridlines. Their symmetry group has two elements, the identity and the reflection in a line parallel to the sides of the squares.

• 26 nonominoes have an axis of reflection symmetry at 45° to the gridlines. Their symmetry group has two elements, the identity and a diagonal reflection.

• 19 nonominoes have point symmetry, also known as rotational symmetry of order 2. Their symmetry group has two elements, the identity and the 180° rotation.

• 4 nonominoes have two axes of reflection symmetry, both aligned with the gridlines. Their symmetry group has four elements, the identity, two reflections and the 180° rotation. It is the dihedral group of order 2, also known as the Klein four-group.

• 2 nonominoes have four axes of reflection symmetry, aligned with the gridlines and the diagonals, and rotational symmetry of order 4. Their symmetry group, the dihedral group of order 4, has eight elements.

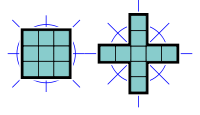
Unlike octominoes, there are no nonominoes with rotational symmetry of order 4 or with two axes of reflection symmetry aligned with the diagonals.

If reflections of a nonomino are considered distinct, as they are with one-sided nonominoes, then the first and fourth categories above double in size, resulting in an extra 1,215 nonominoes for a total of 2,500. If rotations are also considered distinct, then the nonominoes from the first category count eightfold, the ones from the next three categories count fourfold, the ones from the fifth category count twice, and the ones from the last category count only once. This results in 1,196 x 8 + (38+26+19) x 4 + 4 x 2 + 2 = 9,910 fixed nonominoes.

Packing and tiling

37 nonominoes have holes. Therefore a complete set cannot be packed into a rectangle and some admit no tilings. However, 1050 free nonominoes (all but 235) do admit tilings; of the tiling nonominoes, all but two of them form a patch of at least one tile satisfying the Conway criterion, the two exceptions shown to the right. This is the lowest order of polyomino for which such exceptions exist.
One nonomino has a two-square hole (second rightmost in the top row) and is the smallest polyomino with such a hole.