
- Chess World Cup
- FIDE Grand Prix
- Olympiad
- World Championship
- List of strong tournaments
- List of world championships

- Checkmate patterns
- Chess openings
- Chess strategy
- Chess tactics
- Chess theory
- Endgames
- Pawn structure
- Problems/Compositions












 |
 |
 |
 |
Corresponding squares (also called relative squares, sister squares and coordinate squares) in chess occur in some chess endgames, usually ones that are mostly blocked. If squares x and y are corresponding squares, it means that if one player moves to x then the other player must move to y in order to hold his position. Usually there are several pairs of these squares, and the members of each pair are labeled with the same number, e.g. 1, 2, etc. In some cases they indicate which square the defending king must move to in order to keep the opposing king away. In other cases, a maneuver by one king puts the other player in a situation where he cannot move to the corresponding square, thus the first king is able to penetrate the position (Müller & Lamprecht 2007:188-203). The theory of corresponding squares is more general than opposition, and is more useful in cluttered positions.
Corresponding squares are squares of reciprocal (or mutual) zugzwang. They occur most often in king and pawn endgames, especially with triangulation, opposition, and mined squares. A square that White can move to corresponds to a square that Black can move to. If one player moves to such a square, the opponent moves to the corresponding square to put the opponent in zugzwang (Dvoretsky 2006:15-20).
| a | b | c | d | e | f | g | h | ||
| 8 |

 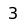 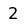  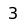    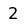 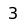 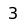 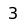 |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
One of the simplest and most important uses of corresponding squares is in this king and pawn versus king endgame. Assume that the black king is in front of the pawn and the white king is behind or to the side of the pawn. The black king is trying to block the white pawn and the white king is supporting its pawn. If the white king gets to any of the key squares (marked with "x"), he wins. Suppose the black king moves to the square labeled "1" near him (square c8). Then if the white king moves to the corresponding square (also labeled "1", square c6), he wins. Conversely, if the white king moves to the "1" square then the black king must move to the corresponding square to draw. Thus if both kings are on the "1" squares, the position is a reciprocal zugzwang. Note that the second player moving to one of the corresponding squares has the advantage. Being on a square when the opponent is not on the corresponding square is a disadvantage.
The squares labeled "2" are similar corresponding squares. If the white king is on the d5 square (the middle one labeled "3"), he is threatening to move to either the "1" square or the "2" square. Therefore the black king must be in a position to move to either his "1" square or his "2" square in order to hold the draw, so he must be on one of his "3" squares. This makes the defense for Black clear: shift between the squares labeled "3" until the white king moves to his "1" or "2" square, and then go to the corresponding square, gaining the opposition. If the black king moves to the "1" or "2" squares under any other circumstances, the white king moves to the corresponding square, takes the opposition, the black king moves, and White advances the pawn and will promote it and win, with a basic checkmate.
The c5 and e5 squares can also be label "3" squares, since if the white king is on one of them, the black king must be on one of his "3" squares to draw.
| a | b | c | d | e | f | g | h | ||
| 8 |

     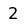  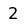  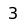 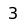 |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
This is another example that is fairly simple. The key squares (see king and pawn versus king endgame) are e1, e2, e3, and f3. If the black king gets to any of those squares, Black wins. The job of the white king is to keep the black king off those squares. One might think that Black has the advantage, since he has the opposition. White can defend the two key squares of e3 and f3 by oscillating between e2 and f2. White's defense is simple if he observes the corresponding squares:
Each time the black king moves to a numbered square, the white king moves to the corresponding square (Müller & Lamprecht 2007:191).
| a | b | c | d | e | f | g | h | ||
| 8 |

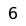 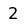  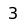      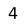 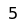     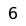 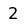 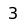 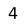  |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
In this position, the squares marked with "x" are key squares and the e1 square is a "5" for White. If White occupies any of the key squares, he wins. With separated key squares, the shortest path connecting them is significant. If White is to move in this position, he wins by seizing a key square by moving to e2 or f2. If Black is to move, he draws by moving to his "5" square. Black maintains the draw by always moving to the square corresponding to the one occupied by the white king (Müller & Lamprecht 2007:188-89).
| a | b | c | d | e | f | g | h | ||
| 8 |

   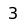  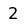  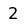   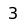   |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
In this position, e2, e3, and d4 are key squares. If the white king can reach any of them, White wins. The black king cannot move out of the "square" of White's d-pawn (see king and pawn versus king endgame), otherwise it will promote. The square c3 is adjacent to d4 and the "1" square the White king is on, so it is numbered "2". Therefore e3 is "2" for Black. White threatens to move to c2, so this is labeled "3". Since Black must be able to move to "1" and "2", f4 is his corresponding "3" square. If the White king is on b2 or b3, he is threatening to move to "2" or to "3", so those are also "1" squares for him. White has more corresponding squares, so he can outmaneuver Black to win (Müller & Lamprecht 2007:189).
White occupies a key square and can support the advance of his pawn until he is able to win the black pawn, e.g.: 6... Kf5 7. Ke3 Ke5 8. d4+ Kd5 9. Kd3 Kd6 10. Ke4 Ke6 11. d5+ Kd6 12. Kd4 Kd7 13. Kc5.
| a | b | c | d | e | f | g | h | ||
| 8 |

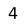 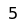 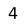  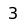 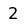   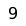 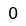 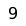   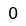 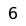 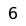           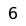 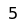 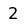 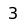 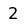   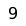 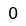 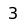 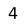 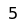 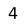    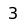    |
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
One of the most famous and complicated positions solved with the method of corresponding squares is this endgame study composed by World Champion Emanuel Lasker and Gustavus Charles Reichhelm in 1901. It is described in the 1932 treatise L'opposition et cases conjuguées sont réconciliées (Opposition and Sister Squares are Reconciled), by Vitaly Halberstadt and Marcel Duchamp.
and White wins by penetrating on the kingside. Each of White's first seven moves are the only one that wins (Müller & Lamprecht 2007:193-94).