Chess handicap

	a	b	c	d	e	f	g	h
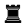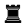8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Initial setup for pawn and move : Black starts without the f-pawn; the weaker player (White) moves first

A handicap (or "odds") in chess is a way to enable a weaker player to have a chance of winning against a stronger one. There are a variety of such handicaps, such as material odds (the stronger player surrenders a certain piece or pieces), extra moves (the weaker player has an agreed number of moves at the beginning of the game), extra time on the chess clock, and special conditions (such as requiring the odds-giver to deliver checkmate with a specified piece or pawn). Various permutations of these, such as "pawn and two moves", are also possible.

Handicaps were quite popular in the 18th and 19th centuries, when chess was often played for money stakes, in order to induce weaker players to play for wagers. Today, except for time odds, handicaps are rarely seen. Rybka, however, a top-rated computer chess engine, played a successful series of handicap matches in 2007 and 2008 against human chess masters.

Some new chess websites offer handicap options to their users. This is an increasingly popular and entertaining game format because it helps bridge the large chess-strength disparity frequently found in online play.

History

According to Harry Golombek, "Odds-giving reached its heyday in the eighteenth century and the early nineteenth century." Indeed, it was so prevalent in the 18th century that Philidor (1726-1795) played the vast majority of his games at odds. About fifteen percent of the known games of Paul Morphy (1837-1884) are games in which he gave odds.

Howard Staunton in The Chess-Player's Handbook (1847) advised inexperienced players to accept odds offered by superior players and, upon improving to the point that they can themselves give odds to some players, to avoid playing such players on even terms, warning that doing so is apt to induce "an indolent, neglectful habit of play". In 1849, Staunton published The Chess-Player's Companion, a 510-page work "chiefly directed to the exposition of openings where one party gives odds". Just over 300 pages were devoted to odds games: Book I (pages 1 to 185) contained games played at various odds, and most of Book V (pages 380-496) discussed various types of odds, including exotic and unusual ones. The late-19th century chess opening treatise Chess Openings Ancient and Modern, by Edward Freeborough and Charles Ranken, included fourteen pages of analysis of best play in games played at odds of pawn and move, pawn and two moves, and either knight.

Macon Shibut writes that in the mid-19th century "chess was a gambling game ... . Individual matches for stakes were the focus of organized play. Matches between leading players attracted a wide following so masters often succeeded in finding sponsors to back their personal wagers." However, the available sums were generally relatively meager, and travel was arduous, so the amount of money obtained in this way was not sufficient to enable professional chess players to support themselves financially. Moreover, the first major chess tournament was not organized until 1851, and chess tournaments remained a rarity for several decades following. With tournaments an unreliable means of making a living, odds-giving became a way for masters to entice amateurs into playing for wagers, since the odds gave the amateur a fighting chance. The odds system even became the earliest rating system: amateurs were graded according to what handicap they needed to compete against a master, and were referred to as a "Rook player" or "Pawn and move player", for example, as we would today speak of players by their Elo ratings (e.g. a "1200 player" or an "1800 player").

The playing of games at odds gradually grew rarer as the nineteenth century proceeded. Today, except for time odds, they have all but disappeared. Shibut posits that games played at material odds became unpopular for (1) technological, (2) political, and (3) philosophical reasons. Taking these in turn, first, the introduction of chess clocks gave rise to a new way to give odds, one that has today supplanted material odds as the preferred mode of odds-giving. Second, the Soviet Union supported chess masters and sponsored chess education, but expected chess masters "to be cultural icons, not hustlers". Third, chess began to be treated in a scientific, logical way, "with an assumption of idealized 'best play' [coming] to underpin all analysis". From this perspective, a game beginning from a "lost" position becomes less interesting, even distasteful. Writings by Wilhelm Steinitz (1836-1900), the first World Champion, and James Mason (1849-1905) are consistent with the last point.

In an interview with Ralph Ginzburg published in the January 1962 issue of Harper's Magazine, future World Champion Bobby Fischer was quoted as saying that women were weak chessplayers and that he could successfully give knight odds to any woman in the world. Fischer later claimed that Ginzburg had distorted what he had said.

In 2001, London businessman Terence Chapman, a master-level player, played a match against former World Champion Garry Kasparov, with Kasparov giving odds of two pawns in each game (the pawns removed were different each time); Kasparov won the match by two games to one, with one draw.

Rybka, a top-rated computer chess engine designed by International Master Vasik Rajlich, played a series of handicap matches against strong human players. In March 2007, Rybka defeated Grandmaster Jaan Ehlvest after giving pawn odds (removing a different pawn each time). In January 2008, Rybka defeated Grandmaster Joel Benjamin after giving draw odds. On March 2008, Rybka gave pawn and move (removing a different pawn each time) to Grandmaster Roman Dzindzichashvili, drawing the match 4-4. In June 2008, Rybka gave knight odds to FIDE Master John Meyer, losing 4-0. On July 6, 2008, Rybka gave Meyer odds of pawn and three moves, winning 3-1.

Handicaps

The purpose of a handicap, or odds, is to compensate for the difference in skill between two chess players. There are a variety of handicaps: material odds; extra moves; time odds; special restrictions (such as pion coiffé); weighting of results (such as "draw odds" - counting a draw as a loss for the odds-giver); differential stakes; and physical restrictions, such as blindfold chess. Many different permutations of handicaps (for example, a material handicap plus time odds) are also possible, as are countervailing handicaps (for example, a player gives up a piece, but receives one of the opponent's pieces or pawns and/or extra moves, in return).

Main

Harry Golombek gives the following list of material odds (in increasing handicap level):

Note that the odds-giver plays White unless otherwise indicated, and "pawn odds" normally refers to the f-pawn (i.e. the pawn initially located on the f2-square for White, and on the f7-square for Black).

• Odds of the move: The weaker player plays White.
• Two moves: The weaker player plays White and starts the game by making two moves.
• Pawn and move: The weaker player plays White; a black pawn (typically that on f7) is removed from the board.
• Pawn and two moves: The weaker player plays the first two moves, and Black's pawn on f7 is removed.
• Knight odds: One of the stronger player's knights is removed, usually the queen knight on b1.
• Rook odds: One of the stronger player's rooks is removed, usually the queen rook on a1.
• Rook and pawn: The stronger player's queen rook and f-pawn are removed.
• Two minor pieces: The odds-giver chooses which of their two knights and/or bishops to remove.
• Rook and knight: The stronger player's queen rook and queen knight are removed.
• Queen odds: The stronger player's queen is removed.
• Two rooks: Both rooks of the stronger player are removed.
• Strong king: The weaker player's king may move up to two squares in any direction in a straight line.

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

White mates in two moves regardless what Black plays

Larry Kaufman writes that under the chess tradition of the 18th and 19th centuries, the handicap below knight odds was:

• Pawn and three moves: White plays the first three moves, and Black plays without the f7-pawn. In odds games with extra moves (pawn and two moves, pawn and three moves), the odds-receiver cannot move beyond the fourth rank with those moves. Otherwise, White could win immediately with 1.e3 2.Bd3 3.Qh5+ g6 4.Qxg6+ hxg6 5.Bxg6#.

Even with the "no moves beyond the fourth rank" proviso, Black cannot give White an unlimited number of moves. Doing so would allow White to set up the position at right, when White's dual threats of 1.Qxf7# and 1.Ned6+ cxd6 2.Nxd6# are immediately decisive.

I.A. Horowitz adds to the above list the following:

• Draw odds: The smallest of these handicaps; the stronger player plays White, and draws are counted as wins for Black.
• Queen for a rook: A handicap between knight odds and rook odds; the odds-giver's queen, and the odds-receiver's queen rook, are removed.
• Queen for a knight: A handicap slightly greater than rook odds; the odds-giver's queen, and the odds-receiver's queen knight, are removed.

If a rook is given, the player giving the odds can still castle with the absent rook, moving only the king.

Others

Time handicaps are most often practiced in blitz games. The stronger player may be given one or two minutes to play the whole game, while the weaker player receives five minutes or more. Money odds are another way of compensating for a difference in strength; the stronger player puts up some multiple (three, five, ten, etc.) of the amount of money put up by the weaker player.

In the 16th-19th centuries pion coiffé (capped or marked pawn) handicapping was sometimes used. The stronger player must checkmate with a particular pawn, which is usually marked at the start of play. The pawn cannot be promoted; giving checkmate with any other pawn or piece loses the game. Pion coiffé is considered to be about equivalent to giving odds of a queen. Similarly, games have occasionally been played with a ringed piece, where a ring or band is placed around a particular piece, and the player giving odds must checkmate with that piece. This form of odds, along with pion coiffé, are very difficult for the odds-giver, who cannot allow the odds-receiver to sacrifice for the capped or ringed piece or pawn. For instance, in pion coiffé, after 1.e4 d5 2.exd5 Qxd5, Black already threatens to sacrifice the queen for the capped pawn if it is the a-, d-, or g-pawn, to play 3...Qe5+ followed by such a sacrifice if it is the b- or h-pawn, or to play 3...Qe4+ followed by a sacrifice if it is the c-pawn.

• Checkmate on a particular square: This may mean either that the odds-receiver's king must be mated while on the specified square, or that the odds-giver's piece must administer mate from that square. Carrera considered the first of these roughly equivalent to knight odds, the second a bit less. Assiac observed of the first, "This sounds like a formidable proposition, but it really isn't. All the better player has to do is reduce the game to a favorable ending. Thereafter, having promoted a pawn or two, he will find the rest easy."
• Checkmate with a pawn: The mating pawn may be any pawn, not a specified pawn, as in pion coiffé. Carrera considered this form of odds equivalent to giving odds of two pawns.
• Giving all the pieces for two moves each time: The odds-giver begins the game with only the king and pawns, while the odds-receiver has a full complement of pieces and pawns. In exchange for this, the odds-giver plays two moves on each turn, while the odds-receiver can only play one. Carrera wrote that while some considered this an even game, he thought that it favored the pieces, although the side with the pieces must play cautiously. The player with the pieces should try to eliminate the pawns, for instance by giving up two pawns for one, or a minor piece for two pawns.
• Giving the king the knight's move: The odds-receiver's king, in addition to being able to move in the usual manner, is able to move like a knight. Carrera considered this form of odds improper because it allows the odds-receiver to use his king to checkmate the enemy king from a knight's move away (for example, with the odds-receiver's king at g6 and the odds-giver's king at h8, the latter is in check and, if no legal response is possible, is checkmated). Carrera considered this form of odds equivalent to giving rook and pawn odds. Because of the king's unusual power, the odds-giver requires more material than usual in order to checkmate a bare king (for example, queen and another piece, or two rooks).
• Giving the queen the knight's move: Similarly to the above, the odds-receiver's queen (rather than king) has the additional ability to move like a knight. This makes the queen very powerful, since she has the ability to administer mate without the assistance of any other pieces (for instance, an enhanced queen on h6 mates a king on h8, since Kg8 would still leave the king in check). Carrera considered this roughly equivalent to knight odds, although it varied depending on the players' strengths.
• Odds of the castled king The odds-receiver begins the game with the positions of his king and one of his rooks interchanged (e.g., king on h8 or a8, and the displaced rook on the king's square). The first way (king on h8, rook on e8) is used unless otherwise specified before the game. Carrera thought this form of odds equivalent to the player with normally placed pieces giving a little less than two pawns, or a little less than a knight if the a8-rook and king are the ones interchanged. Staunton noted that Carrera's description and examples of these odds "are not adapted to our mode of castling" since the king and rook do not end up on the same squares they would normally occupy after castling.

Staunton also mentioned the following unusual forms of odds not discussed by Carrera:

• Odds of the losing game: The odds-giver undertakes to force the odds-receiver to checkmate him. (See Paris-Marseilles, correspondence 1878, given below.)
• Additional pawns: The odds-giver permits the odds-receiver to begin the game with a specified number of extra pawns (for example, eight extra pawns). Unless specially agreed, the side with the extra pawns moves first.
• Odds of queen rook in exchange for the opponent's queen knight, or pawn and move, or pawn and two moves.
• Odds of queen knight in exchange for pawn and move, or in exchange for the first two moves.

Rating equivalent

Grandmaster Larry Kaufman wrote the following about the Elo rating equivalence of giving knight odds:

[T]he Elo equivalent of a given handicap degrades as you go down the scale. A knight seems to be worth around a thousand points when the "weak" player is around IM level, but it drops as you go down. For example, I'm about 2400 and I've played tons of knight odds games with students, and I would put the break-even point (for untimed but reasonably quick games) with me at around 1800, so maybe a 600 value at this level. An 1800 can probably give knight odds to a 1400, a 1400 to an 1100, an 1100 to a 900, etc. This is pretty obviously the way it must work, because the weaker the players are, the more likely the weaker one is to blunder a piece or more. When you get down to the level of the average 8 year old player, knight odds is just a slight edge, maybe 50 points or so.

Kaufman has written that Kasparov could give pawn and move odds to a low grandmaster (2500 FIDE rating) and be slightly favored, and would have even chances at knight odds against a player with a FIDE rating of 2115.

Illustrative games

Eckart-Tarrasch, 1887-88

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 13...Rxd4

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 16.Nc3

Pawn and move
This game was won by Siegbert Tarrasch, whom Assiac described as "one of the greatest experts of 'Pawn and move' theory":

K. Eckart-Tarrasch, Nuremberg Chess Club Championship 1887-88 (remove Black's f-pawn)
1. e4 Nc6 2. f4 e5 3. Nf3 exf4 4. Bc4 Bc5 Planning the following unsound but tricky sacrifice. 5. d4 Nxd4?! 6. Nxd4 Qh4+ 7. Kf1 d5 Sacrificing another pawn for rapid development. 8. exd5 Bg4 9. Bb5+? Evidently overlooking Black's next move. Correct was 9.Qd3, with a satisfactory defense. c6! 10. dxc6 0-0-0! 11. cxb7+ Kxb7 12. Bc6+ Kb6 13. Qd3 Rxd4 Black has regained the sacrificed piece and, contrary to appearances, his king is quite safe. 14. Qb5+ Kc7 15. Qb7+ Kd6 16. Nc3 Allowing a pretty finish, but 16.Bf3 Rd1+! 17.Ke2 (17.Bxd1 Qf2#) Bxf3+ 18.Qxf3 Rxh1 also wins for Black. Qf2+! 17. Kxf2 Rd1+ (discovered check) 18. Be3 Bxe3# 0-1 Notes based on those by Fred Reinfeld.

Zukertort-Epureanu, 1872

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 19...Ne7

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position; Black, ahead a queen, bishop, and knight, is defenseless.

Knight odds
Johannes Zukertort-Epureanu, Berlin 1872 (remove White's queen knight)
1. f4 e6 2. Nf3 Nf6 3. b3 d5 4. Bb2 c5 5. e3 Nc6 6. a3 a6 7. Bd3 Bd6 8. Qe2 0-0 9. g4 Nxg4? Imprudently allowing White to attack Black's king along the g-file. 10. Qg2 Nf6 11. h4 h6 12. h5 Kh8 13. 0-0-0 Ne8 14. Rdg1 Rg8 15. Bh7!! f6 (15...Kxh7 16.Qg6+!! fxg6 17.hxg6+ Kh8 18.Rxh6#) 16. Bxg8 Kxg8 17. Qg6 Kh8 18. Ng5! hxg5 19. fxg5 Ne7 20. gxf6!! Nxg6 21. hxg6+ Kg8 22. Rh8+! Kxh8 23. f7 1-0 There is no defense against mate. If 23...Qh4 (stopping the threatened 24.Rh1+), 24.fxe8(Q)+ Bf8 25.Qxf8#. Francis J. Wellmuth calls this "the finest odds-game ever played". Irving Chernev and Fred Reinfeld call the conclusion "the finest finish in this type of contest." Notes by Chernev and Reinfeld, Wellmuth, and Napier.

Kashdan-Horneman, 1930

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 13...f6?

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position after 16.Ng7#

Rook odds
Isaac Kashdan-Buster Horneman, Manhattan Chess Club 1930 (remove White's queen rook)
1. e4 e6 2. d4 d5 3. e5 c5 4. Qg4 cxd4 5. Nf3 Nh6 6. Qh3 Be7 7. Bd3 b6 8. Qg3 Nf5 9. Bxf5 exf5 10. Qxg7 Rf8 11. Nxd4 Ba6? 12. Nxf5 Nd7 13. Bg5 f6? 14. e6! fxg5 15. Qg6+!! hxg6 16. Ng7# 1-0

Morphy-Maurian, 1855

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 9.Qe2

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position after 12...Ng4#

It would be a mistake to suppose that the odds-giver always wins. Even the strongest players sometimes meet with disaster:

Paul Morphy-Charles Maurian, Springhill 1855 (remove White’s queen rook)
1. e4 e5 2. f4 exf4 3. Bc4 Qh4+ 4. Kf1 b5 5. Bd5 Nc6 6. Nf3 Qh5 7. d4 Nf6 8. Bb3 Ba6 9. Qe2 Nxd4! 10. Nxd4 b4! 11. Qxa6?? Qd1+ 12. Kf2 Ng4# 0-1

Apscheneek-Amateur, 1934

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 21...Rad8

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position after 25.Nh6#

Queen odds
Apscheneek-Amateur, Riga 1934 (remove White's queen)
1. b3 e5 2. Bb2 d6 3. Nc3 Be7 4. 0-0-0 Nf6 5. f3 0-0 6. e3 c6 7. g4 h6 8. Nge2 Be6 9. Ng3 Nbd7 10. h4 Nh7 11. g5 hxg5 12. hxg5 Bxg5 13. Bd3 Bh6 14. Rdg1 d5 15. Nf5 Bxf5 16. Bxf5 Qf6 17. Bxd7 d4 18. exd4 exd4 19. Ne2 Qe7 20. Nxd4 Qxd7 21. Rxh6 Rad8 22. Rxg7+! Kxg7 23. Nf5+ (double check) Kg8 24. Rg6+! fxg6 25. Nh6# 1-0

Lange-von Schierstedt, 1856

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 14.Raf1

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position: the ringed knight mates.

Ringed piece
Max Lange-Jenny von Schierstedt, Halle 1856 (White's queen knight is the ringed piece with which he must checkmate)
1. e4 e5 2. Nc3 Nc6 3. f4 exf4 4. Nf3 g5 5. Bc4 g4 6. 0-0 gxf3 7. d4 fxg2 8. Bxf7+ Kxf7 9. Qh5+ Kg7 10. Rxf4 Nh6 11. Be3 d6 12. Ne2 Qe7 13. Kxg2 Be6 14. Raf1 Bf7? Black could have won with 14...Qg5+!!, when 15.Qxg5 would checkmate Black, but violate the stipulation that the queen knight must checkmate. 15. Qxh6+!! Kxh6 16. Rg4+ Kh5 17. Ng3+ Kxg4 18. Rf5 h6 19. h3+ Kh4 20. Rh5+ Bxh5 21. Nf5# 1-0

Staunton-Taverner

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 3.Ng3; White guards the capped pawn against frontal attack.

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position; the capped pawn gives mate.

Pion coiffé
Howard Staunton-Taverner?, date unknown (White's pawn on g2 is the capped pawn, with which he must give checkmate)
1. Nc3 e5 2. Ne4 d5 3. Ng3 Covering the pawn to make it less assailable by Black's pieces. f5 4. e3 Bd6 5. c4 h5 6. Nxh5 Qg5 7. Ng3 f4 8. exf4 Not 8.Nf3??, when 8...Bh3! would win the g-pawn and the game. exf4 9. d4 Qg6 10. Bd3 Qh6 Now Black threatens 11...Qh3! and wins. 11. Qh5+ Qxh5 12. Nxh5 Rxh5 13. Bg6+ Ke7 14. Bxh5 Nf6 15. Bf3 g5 16. c5 g4 17. cxd6+ cxd6 18. Bxg4 Bxg4 19. Bxf4 Nh5 20. Bg3 Nc6 21. h3 21.f3? Be6 22.Ne2 Rg8 23.Kf2 Bh3! 24.gxh3 Nxg3 followed by 25...Rh8 would win the capped pawn. Be6 22. Ne2 Rg8 23. Rc1 Bf5 24. Rc3 Be4 25. Re3 Nb4 26. Kd2 Nxa2 27. Ra1 Nb4 28. Rxa7 Nc6 29. Rxb7+ Ke6 30. Rh7 Rg5 31. Rxe4+ dxe4 32. Rxh5 Rxh5 33. Nf4+ Ke7 34. Nxh5 Nxd4 35. Ke3 Nc2+ 36. Kxe4 Ne1 Attacking the "game pawn". 37. Bh4+ Kd7 38. g4 Kc6 39. f4 Nc2 40. f5 d5+ 41. Kf4 d4 42. Bf2 d3 43. Be3 Nd4 44. Ke4 d2 45. Bxd2 Nb3 46. Be3 Kd6 47. Nf6 Kc6 48. h4 Na5 49. h5 Nc4 50. Bf4 Nxb2 51. h6 Na4 52. h7 Nc5+ 53. Ke3 Kb5 54. Ne4 Na6 55. h8=Q Ka5 56. Qc3+ Kb5 57. Qb3+ Ka5 58. Nc3 Nc5 59. Bc7+ Ka6 60. Qb5+ Ka7 61. Qxc5+ Ka6 Deliberately allowing checkmate. 62. Qa5+ Kb7 63. Ke4 Kc8 64. Qa7 Kd7 65. Qb7 Ke7 66. Qc8 Kf6 67. Bd8+ Kg7 68. Qe6 Kf8 69. Qe7+ Kg8 70. Nd5 Kh8 71. g5 Kg8 72. g6 Kh8 73. Ke5 Kg8 74. Nf6+ Kh8 75. g7# 1-0 Notes by Staunton, who wrote that he and his opponent played many games at these odds, of which this was "perhaps the weakest, but ... also the shortest".

Paris-Marseilles, 1878

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Position after 67.Kb1

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h Final position; Black, having forced White to give checkmate, wins.

Odds of queen in return for requiring Black to force White to checkmate
Paris-Marseilles, correspondence 1878 (remove White's queen; in response for receiving the queen, Black undertakes to force White to checkmate Black)
1. d4 d5 2. Nc3 c6 3. Nf3 g6 4. e4 e6 5. e5 Bb4 6. Bd2 Bxc3 7. Bxc3 b5 8. h4 h5 9. 0-0-0 a6 10. Ng5 f5 11. g3 Nh6 12. Bd3 Nf7 13. Bxf5? gxf5 14. Nxf7 Kxf7 15. Bd2 Nd7 16. Rhe1 c5 17. dxc5 Nxc5 18. Bg5 Qg8 19. Re3 Bb7 20. Rc3 Rc8 21. Be3 Nd7 22. Bd4 Rxc3 23. bxc3 a5 24. Kd2 a4 25. Rb1 Ba6 26. Rg1 Qg4 27. Rb1 Rc8 28. Rb4 Rc4 29. Rxc4 dxc4 30. a3 f4 31. Kc1 fxg3 32. fxg3 Qxg3 33. Kb2 Qxh4 34. Kc1 Qe1+ 35. Kb2 Qd1 36. Ba7 Nxe5 37. Bc5 h4 38. Bd4 Nc6 39. Be3 e5 40. Bf2 h3 41. Bg3 e4 42. Bf4 Ke6 43. Bg3 e3 44. Bf4 e2 45. Bg3 Kd7 46. Bh2 e1=Q 47. Bf4 Qee2 48. Bg3 Qdxc2+ 49. Ka1 Qf1+ 50. Be1 Qd2 Now White is reduced to shuffling the king back and forth while Black sets up self-mate. 51. Kb1 h2 52. Ka1 h1=Q 53. Kb1 Qf8 54. Ka1 Qxa3+ 55. Kb1 Qad6 56. Ka1 Qf6 57. Kb1 Kc7 58. Ka1 b4 59. Kb1 b3 60. Ka1 Kb6 61. Kb1 Ka5 62. Ka1 Ne7! 63. Kb1 Nc8 64. Ka1 Bb5 65. Kb1 Qa6! 66. Ka1 Nb6 67. Kb1 Qh7+ 68. Ka1 Qxc3+! 69. Bxc3# The only legal move. 0-1 Black, having forced White to checkmate, wins.